题目内容
已知-π<x<0,sin(x+
)-sin(π+x)=
,求tanx的值.
| π |
| 2 |
| 1 |
| 5 |
考点:运用诱导公式化简求值,同角三角函数间的基本关系
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系、诱导公式求得sinx和cosx的值,可得tanx=
=-
| sinx |
| cosx |
解答:
解:∵-π<x<0,sin(x+
)-sin(π+x)=cosx+sinx=
,∴1+2sinxcosx=
,sinxcosx=-
<0.
∴cosx>0,sinx<0,|cosx|>|sinx|,cosx>-sinx,∴tanx∈(-1,0).
再根据sin2x+cos2x=1,可得sinx=-
,cosx=
,∴tanx=
=-
.
| π |
| 2 |
| 1 |
| 5 |
| 1 |
| 25 |
| 12 |
| 25 |
∴cosx>0,sinx<0,|cosx|>|sinx|,cosx>-sinx,∴tanx∈(-1,0).
再根据sin2x+cos2x=1,可得sinx=-
| 3 |
| 5 |
| 4 |
| 5 |
| sinx |
| cosx |
| 3 |
| 4 |
点评:本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,判断cosx>0,sinx<0,是解题的关键,属于基础题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
在△ABC中,D为边BC的中点,则下列向量关系式正确的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
二次函数y=x2+bx与指数函数y=bx的图象只可能是( )
A、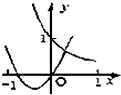 |
B、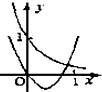 |
C、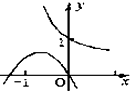 |
D、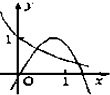 |



