Question

某农户计划种植黄瓜和韭菜，种植面积不超过50亩，投入资金不超过54万元，假设种植黄瓜和韭菜的产量、成本和售价如下表：

	年产量/亩	年种植成本/亩	每吨售价
黄瓜	4吨	1.2万元	0.55万元
韭菜	6吨	0.9万元	0.3万元

问该农户如何安排种植计划，才能使一年的种植总利润（总利润=总销售收入-总种植成本）最大，最大总利润是多少万元？

Answer 1

考点：简单线性规划的应用

专题：应用题,不等式的解法及应用

分析：根据条件，设黄瓜和韭菜的种植面积分别为x，y亩，总利润为z万元，建立目标函数和约束条件，根据线性规划的知识求最优解即可．

解答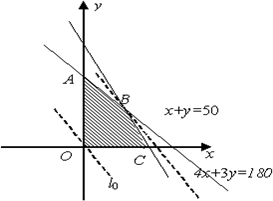： 解：设黄瓜和韭菜的种植面积分别为x，y亩，总利润为z万元，
则目标函数为z=（0.55×4x-1.2x）+（0.3×6y-0.9y）=x+0.9y．
线性约束条件为

x+y≤50 1.2x+0.9y≤54 x≥0，y≥0

，
即

x+y≤50 4x+3y≤180 x≥0，y≥0

，作出不等式组

x+y≤50 4x+3y≤180 x≥0，y≥0

表示的可行域，求得点 A（0，50），B（30，20），C（0，45）．
平移直线z=x+0.9y，可知当直线z=x+0.9y 经过点B（30，20），
即x=30，y=20时，z取得最大值，且Z_max=48（万元）．
故黄瓜和韭菜的种植面积应该分别是30亩、20亩时，利润最大．

点评：本题主要考查生活中的优化问题，利用条件建立二元二次不等式组，利用线性规划的知识进行求解是解决本题的关键．