题目内容
对于实数x,符号[x]不超过x的最大整数,例如[π]=3,[-3.5]=-4,定义函数f(x)=x-[x],则下列结论正确的是( )
| A、方程f(x)=k(k∈R)有且仅有一个解 |
| B、函数f(x)的最大值为1 |
| C、函数f(x)是增函数 |
| D、函数f(x)的最小值为0 |
考点:函数解析式的求解及常用方法
专题:新定义,函数的性质及应用
分析:先充分理解[x]的含义,并对x分类讨论求出函数对应解析式,再画出函数的图象,由图象求出函数的最值、单调性以及周期性,结合答案项进行判断即可.
解答:
解:由题意可知:当x∈[0,1)时,f(x)=x-[x]=x;
当x∈[1,2)时,f(x)=x-[x]=x-1…,
画出函数的图象如下:
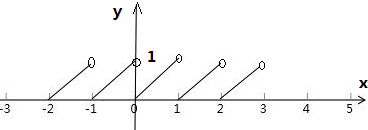
由图得:f(x)=x-[x]∈[0,1),
所以函数f(x)的最小值为0,无最大值,B不对、D正确;
函数图象每隔一个单位重复一次,所以函数是以1为周期的函数,A不对;
函数在定义域有增有减,C不正确.
故选:D.
当x∈[1,2)时,f(x)=x-[x]=x-1…,
画出函数的图象如下:

由图得:f(x)=x-[x]∈[0,1),
所以函数f(x)的最小值为0,无最大值,B不对、D正确;
函数图象每隔一个单位重复一次,所以函数是以1为周期的函数,A不对;
函数在定义域有增有减,C不正确.
故选:D.
点评:本题以新定义的形式考查分段函数的性质:值域、单调性、周期性,利用新定义画出函数的图象是解题的关键,考查数形结合思想和分类讨论思想.

练习册系列答案
相关题目
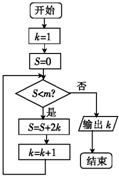 执行如图所示的程序框图,若输出的结果是10,则判断框内m的取值范围是( )
执行如图所示的程序框图,若输出的结果是10,则判断框内m的取值范围是( )| A、(56,72] |
| B、(72,90] |
| C、(90,110] |
| D、(56,90) |
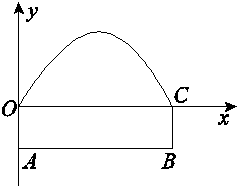 有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?
有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m.现把隧道的横断面放在平面直角坐标系中,若有一辆高为4m,宽为2m的装有集装箱的汽车要通过隧道.问:如果不考虑其他因素,汽车的右侧离开隧道右壁至少多少米才不至于碰到隧道顶部(抛物线部分为隧道顶部,AO、BC为壁)?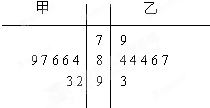 如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.