题目内容
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.

(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.

考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据频率分布直方图,求出样本中男生人数,再由分层抽样比例,估计全校男生人数;
(2)由统计图计算出样本中身高在170~185cm之间的学生数,根据样本数据计算对应的概率;
(3)利用列举法计算基本事件数以及对应的概率.
(2)由统计图计算出样本中身高在170~185cm之间的学生数,根据样本数据计算对应的概率;
(3)利用列举法计算基本事件数以及对应的概率.
解答:
解:(1)根据频率分布直方图,得;
样本中男生人数为2+5+14+13+4+2=40,
由分层抽样比例为10%,
估计全校男生人数为40÷10%=400;
(2)由统计图知,样本中身高在170~185cm之间的学生有
14+13+4+3+1=35人,
样本容量为70,
所以样本中学生身高在170~185cm之间的频率为
f=
=0.5,
由此估计该校学生身高在170~185cm之间的概率为0.5;
(3)样本中身高在180~185cm之间的男生有4人,设其编号为①、②、③、④,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤、⑥;
从上述6人中任取2人的树状图为:
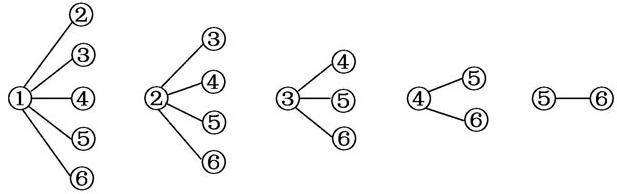
故从样本中身高在180~190cm之间的6名男生中任选2人的所有可能结果数为15,
至少有1人身高在185~190 cm之间的可能结果数为9,
因此,所求概率P=
=
.
样本中男生人数为2+5+14+13+4+2=40,
由分层抽样比例为10%,
估计全校男生人数为40÷10%=400;
(2)由统计图知,样本中身高在170~185cm之间的学生有
14+13+4+3+1=35人,
样本容量为70,
所以样本中学生身高在170~185cm之间的频率为
f=
| 35 |
| 70 |
由此估计该校学生身高在170~185cm之间的概率为0.5;
(3)样本中身高在180~185cm之间的男生有4人,设其编号为①、②、③、④,
样本中身高在185~190cm之间的男生有2人,设其编号为⑤、⑥;
从上述6人中任取2人的树状图为:

故从样本中身高在180~190cm之间的6名男生中任选2人的所有可能结果数为15,
至少有1人身高在185~190 cm之间的可能结果数为9,
因此,所求概率P=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查了频率分布直方图的应用问题,也考查了用列举法计算古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
已知f(1)=1,f(x)=
(x=2,3,…),m∈N+,则f(2m)=( )
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |
在正四棱锥P-ABCD中,PA=
AB,M是BC的中点,G是△PAD的重心,则在平面PAD中经过点G且与直线PM垂直的直线条数有( )
| ||
| 2 |
| A、0条 | B、1条 | C、3条 | D、无数条 |
 在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,对角线AC=BD=2,且AC⊥BD,则四边形EFGH的面积为
在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,对角线AC=BD=2,且AC⊥BD,则四边形EFGH的面积为 已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.
已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点. 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设