题目内容
2.函数f(x)=3sinx•ln(1+x)的部分图象大致为( )| A. |  | B. |  | C. | 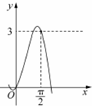 | D. |  |
分析 根据函数值的符号和导数和函数的极值的关系即可判断.
解答 解:由f(x)=3sinx•ln(x+1)知x>-1,
当x=$\frac{π}{2}$时,f($\frac{π}{2}$)=3sin$\frac{π}{2}$ln($\frac{π}{2}$+1)=3ln($\frac{π}{2}$+1)<3lne=3,
∵f′(x)=3cosxln(x+1)+3sinx•$\frac{1}{x+1}$,
令f′(x)=0,
即3cosxln(x+1)+3sinx•$\frac{1}{x+1}$=0,
当0<x<π时,ln(x+1)>0,sinx>0,$\frac{1}{x+1}$>0,
∴cosx<0,
∴$\frac{π}{2}$<x<π,
∴函数的极值点在($\frac{π}{2}$,π),
故选:B.
点评 本题考查了函数图象的识别,根据根据函数值的符号即可判断,属于基础题.

练习册系列答案
相关题目
14.函数f(x)=Asin(ωx+$\frac{ωπ}{2}$)(A>0,ω>0)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,则ω的最大值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{11}$ |