题目内容
12．与向量$\overrightarrow{a}$=（4，-3）垂直的单位向量是（$\frac{3}{5}$，$\frac{4}{5}$）．分析 根据相互垂直的两个向量的数量积为0便可看出向量（3，4）与$\overrightarrow{a}$垂直，从而将向量（3，4）变成单位向量即可．
解答 解：可看出向量（3，4）⊥（4，-3）；
∴与向量$\overrightarrow{a}=（4，-3）$垂直的单位向量为$（\frac{3}{5}，\frac{4}{5}）$．
故答案为：$（\frac{3}{5}，\frac{4}{5}）$．
点评 考查相互垂直的两个向量的数量积为0，单位向量的概念，以及将一个向量变成单位向量的方法．
练习册系列答案
相关题目
3．若方程x3-3ax+2=0（a＞0）有三个不同的实根，则实数a的取值范围为（ ）
| A． | a＞0 | B． | 0＜a＜1 | C． | 1＜a＜3 | D． | a＞1 |
20．设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的向量，已知向量$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+sinα$\overrightarrow{{e}_{2}}$（-$\frac{π}{2}$＜α＜$\frac{π}{2}$），$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\frac{5}{4}$$\overrightarrow{{e}_{2}}$，$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，若A、B、D三点共线，则函数f（x）=2cos（x+α）在[0，π）上的值域为（ ）
| A． | [-1，$\frac{1}{2}$] | B． | [-2，$\sqrt{3}$] | C． | （-2，1] | D． | （-1，$\sqrt{3}$] |
18．
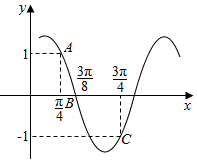已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若tanα=3，则f（$α+\frac{π}{8}$）的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若tanα=3，则f（$α+\frac{π}{8}$）的值为（ ）| A． | -$\frac{3}{5}$ | B． | -$\frac{4}{5}$ | C． | -$\frac{3\sqrt{2}}{5}$ | D． | -$\frac{4\sqrt{2}}{5}$ |