题目内容
7．已知数列{an}满足a1=10，且2an+1=2an-3，若ak•ak+1＜0，则正整数k=（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
分析 利用2an+1=2an-3，判断数列{an}是等差数列，求出数列的通项，确定其正数项，即可得到结论
解答 解：因为2an+1=2an-3，所以an+1-an=-$\frac{3}{2}$，
所以数列{an}是首项为10，公差为-$\frac{3}{2}$的等差数列，所以an=10-$\frac{3}{2}$（n-1），
由an=10-$\frac{3}{2}$（n-1）＞0，得n＜7$\frac{2}{3}$，
所以使akak+1＜0的k值为7，
故选：B．
点评 本题考查等差数列的判定，考查数列的通项，考查学生的计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在直三棱柱ABC-A1B1C1中，D为AC的中点，∠ABC=90°，AA1=AB=2，BC=3．
18．设p、q是两个命题，若￢（p∨q）是真命题，那么（ ）
| A． | p是真命题且q是假命题 | B． | p是真命题且q是真命题 | ||
| C． | p是假命题且q是真命题 | D． | p是假命题且q是假命题 |
15．已知四边形ABCD的对角线相交于一点，$\overrightarrow{AC}$=（1，$\sqrt{3}$），$\overrightarrow{BD}$=（-$\sqrt{3}$，1），则$\overrightarrow{AB}$•$\overrightarrow{CD}$的取值范围是（ ）
| A． | （0，2） | B． | （0，4] | C． | [-2，0） | D． | [-4，0） |
12．现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如图，则按照从左到右的顺序，图象对应的函数序号正确的一组是（ ）
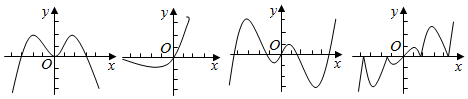
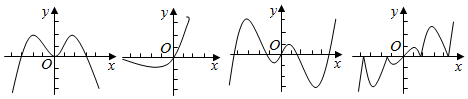
| A． | ①④③② | B． | ①④②③ | C． | ④①②③ | D． | ③④②① |
16．在△ABC中，BC=1，ccosA+acosC=2bcosB，△ABC的面积S=$\sqrt{3}$，则AC等于（ ）
| A． | $\sqrt{13}$ | B． | 4 | C． | 3 | D． | $\sqrt{15}$ |