题目内容
10.已知$α∈(\frac{π}{2},π)$,$cos2α=sin(\frac{π}{4}-α)$,则sin2α=-$\frac{1}{2}$,sinα=$\frac{\sqrt{6}+\sqrt{2}}{4}$.分析 由题意可得cosα+sinα=$\frac{\sqrt{2}}{2}$,平方求得sin2α的值,可得2α的值,从而求得α的值,进而求得sinα的值.
解答 解:∵$α∈(\frac{π}{2},π)$,∴2α∈(π,2π),
∵$cos2α=sin(\frac{π}{4}-α)$,即cos2α=(cos2α-sin2α)=$\frac{\sqrt{2}}{2}$(cosα-sinα)<0,
∴2α∈(π,$\frac{3π}{2}$),
∴cosα+sinα=$\frac{\sqrt{2}}{2}$,或 cosα-sinα=0(舍去).
∴只有cosα+sinα=$\frac{\sqrt{2}}{2}$,∴1+sin2α=$\frac{1}{2}$,sin2α=-$\frac{1}{2}$.
此时,2α=$\frac{11π}{6}$(舍去)或$\frac{7π}{6}$;
∵α=$\frac{7π}{12}$,
∴sinα=sin($\frac{7π}{12}$)=sin($\frac{π}{3}$+$\frac{π}{4}$)=sin$\frac{π}{3}$cos$\frac{π}{4}$+cos$\frac{π}{3}$sin$\frac{π}{4}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
故答案为:-$\frac{1}{2}$;$\frac{\sqrt{6}+\sqrt{2}}{4}$.
点评 本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.将函数y=3sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{2}$个单位后,得到的图象对应函数为g(x),则g($\frac{π}{6}$=)( )
| A. | 0 | B. | -3 | C. | 3 | D. | $\frac{3}{2}$ |
18.设p、q是两个命题,若¬(p∨q)是真命题,那么( )
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是假命题且q是假命题 |
15.已知四边形ABCD的对角线相交于一点,$\overrightarrow{AC}$=(1,$\sqrt{3}$),$\overrightarrow{BD}$=(-$\sqrt{3}$,1),则$\overrightarrow{AB}$•$\overrightarrow{CD}$的取值范围是( )
| A. | (0,2) | B. | (0,4] | C. | [-2,0) | D. | [-4,0) |
20.设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的向量,已知向量$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+sinα$\overrightarrow{{e}_{2}}$(-$\frac{π}{2}$<α<$\frac{π}{2}$),$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\frac{5}{4}$$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,若A、B、D三点共线,则函数f(x)=2cos(x+α)在[0,π)上的值域为( )
| A. | [-1,$\frac{1}{2}$] | B. | [-2,$\sqrt{3}$] | C. | (-2,1] | D. | (-1,$\sqrt{3}$] |
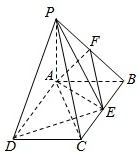 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.