题目内容
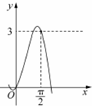
14.函数f(x)=Asin(ωx+$\frac{ωπ}{2}$)(A>0,ω>0)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,则ω的最大值是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{11}$ |
分析 求出f(x)的单调增区间,根据集合关系列出不等式解出ω.
解答 解:令-$\frac{π}{2}$ωx+$\frac{ωπ}{2}$≤$\frac{π}{2}$,解得-$\frac{π}{2}$-$\frac{π}{2ω}$+$\frac{2kπ}{ω}$≤x≤-$\frac{π}{2}$+$\frac{π}{2ω}$+$\frac{2kπ}{ω}$.
∵f(x)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,
∴-$\frac{π}{2}$-$\frac{π}{2ω}$+$\frac{2kπ}{ω}$≤-$\frac{3π}{4}$,①
-$\frac{π}{2}$+$\frac{π}{2ω}$+$\frac{2kπ}{ω}$≥-$\frac{π}{6}$,②
∴解得:$\left\{\begin{array}{l}{ω≤2-8k}\\{ω≤\frac{3}{2}+6k}\end{array}\right.$,
∴当2-8k≤$\frac{3}{2}$即k≥$\frac{1}{28}$时,ω≤2-8k,
∴当k=1时,ω取得最大值-6.
当2-8k>$\frac{3}{2}$+6k,即k<$\frac{1}{28}$时,ω≤$\frac{3}{2}$+6k,
∴当k=0时,ω取得最大值$\frac{3}{2}$.
综上,ω的最大值为$\frac{3}{2}$.
故选:A.
点评 本题考查的知识点是正弦型函数的单调性,三角函数的值,其中根据已知分析出ω的范围是解答的关键,属于中档题.

练习册系列答案
相关题目
6.设P(x,y)满足约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x+y≤3}\end{array}\right.$,则点P对应的区域与坐标轴围成的封闭图形面积为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{11}{2}$ |
3.若方程x3-3ax+2=0(a>0)有三个不同的实根,则实数a的取值范围为( )
| A. | a>0 | B. | 0<a<1 | C. | 1<a<3 | D. | a>1 |
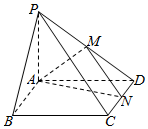 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点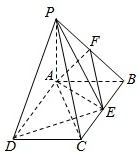 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.