题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，已知
=
，且C=
．
（1）求角A，B的大小；
（2）设函数f（x）=sin（2x+A）-sin2x+cos2x，求函数f（x）的最小正周期及单调递减区间．
| cosA |
| cosB |
| b |
| a |
| 2π |
| 3 |
（1）求角A，B的大小；
（2）设函数f（x）=sin（2x+A）-sin2x+cos2x，求函数f（x）的最小正周期及单调递减区间．
考点：正弦定理的应用,三角函数中的恒等变换应用
专题：三角函数的求值,三角函数的图像与性质,解三角形
分析：（1）由题意及正弦定理可得sin2A=sin2B，可得A=B，即可求得角A，B的大小；
（2）化简解析式可得f（x）=
sin（2x+
），从而可求函数f（x）的最小正周期及单调递减区间．
（2）化简解析式可得f（x）=
| 3 |
| π |
| 3 |
解答：
解：（1）∵
=
，由正弦定理可得
=
=
，
即sin2A=sin2B，
∴A=B或A+B=
（舍去），
又∠C=
，所以，A=B=
．
（2）f（x）=sin（2x+A）-sin2x+cos2x=sin（2x+
）+cos2x，
=sin2xcos
+cos2xsin
+cos2x，
=
sin2x+
cos2x=
sin（2x+
），
所以，最小正周期为T=
=π，
令2kπ+
＜2x+
＜2kπ+
（k∈Z），得kπ+
＜x＜kπ+
（k∈Z），
所以，函数函数f（x）的单调递减区间[kπ+
，kπ+
]，（k∈Z）．
| cosA |
| cosB |
| b |
| a |
| cosA |
| cosB |
| b |
| a |
| sinB |
| sinA |
即sin2A=sin2B，
∴A=B或A+B=
| π |
| 2 |
又∠C=
| 2π |
| 3 |
| π |
| 6 |
（2）f（x）=sin（2x+A）-sin2x+cos2x=sin（2x+
| π |
| 6 |
=sin2xcos
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
所以，最小正周期为T=
| 2π |
| |ω| |
令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
所以，函数函数f（x）的单调递减区间[kπ+
| π |
| 12 |
| 7π |
| 12 |
点评：本题主要考查了三角函数中的恒等变换应用，正弦定理的应用，三角函数的图象与性质，属于基本知识的考查．
练习册系列答案
相关题目
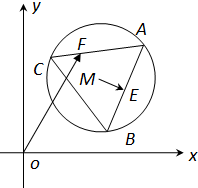如图，已知圆M：（x-3）2+（y-3）2=4，△ABC为圆M的内接正三角形，E为边AB的中点，当正△ABC绕圆心M转动，同时点F在边AC上运动时，已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
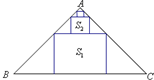在等腰直角△ABC中，∠A=90°，BC=3，△ABC中排列着内接正方形，如图所示，若正方形的面积依次为S1，S2，…，Sn，…（从大到小），其中n∈N*，则