题目内容
当百位和个位上的数字相同且大于十位上的数字时，称这样的数为“三位伞数”，从“三位伞数”中取出一个，则这个数小于300的概率为 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：分9种情形处理，计算出三位伞数的种数，再求出小于300的三位伞数的个数，根据概率公式计算即可
解答：
解：分9种情形处理，当十位数字为0时，百位、个位的数字为有9种选法，
当十位数字为1时，百位、个位的数字为8种选法，
当十位数字为2时，百位、个位的数字为7种选法，
…，
当十位数字为8时，百位、个位的数字为1种选法，
故“三位伞数”共有1+2+…+8+9=45个，
而小于300的伞数共有101，212，202共3个，
故所求概率为
=
．
故答案为：
．
当十位数字为1时，百位、个位的数字为8种选法，
当十位数字为2时，百位、个位的数字为7种选法，
…，
当十位数字为8时，百位、个位的数字为1种选法，
故“三位伞数”共有1+2+…+8+9=45个，
而小于300的伞数共有101，212，202共3个，
故所求概率为
| 3 |
| 45 |
| 1 |
| 15 |
故答案为：
| 1 |
| 15 |
点评：本题考查排列、组合的运用以及概率公式的应用；分析题意是要注意到十位数字特殊，要对其进行分类讨论，属于中档题
练习册系列答案
阅读快车系列答案
相关题目
某市缺水问题比较突出，为了制定水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x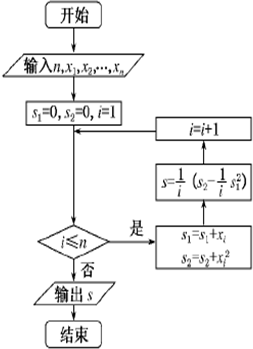
1，x2，…xn（单位：吨），根据如图所示的程序框图，若n=3，且x1，x2，x3，分别为1，2，3，则输出的结果S为（ ）
1，x2，…xn（单位：吨），根据如图所示的程序框图，若n=3，且x1，x2，x3，分别为1，2，3，则输出的结果S为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U=R，集合A={x|x2-x-6≤0}，B={x|
＞0}，那么集合A∩（∁UB）=（ ）
| x+1 |
| x-4 |
| A、{x|-2≤x＜4} |
| B、{x|x≤3或x≥4} |
| C、{x|-2≤x＜-1} |
| D、{x|-1≤x≤3} |
已知集合A={1，2，3}，集合B={x∈Z|1＜x＜4}，则A∩B=（ ）
| A、{2，3} |
| B、{1，4} |
| C、{1，2，3，4} |
| D、∅ |