题目内容
过(-3,2)做抛物线y2=12x切线交抛物线于A、B两点,求直线AB斜率.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设过(-3,2)与抛物线y2=12x相切的直线方程为:y-2=k(x+3),设点A(x1,y1),B(x2,y2).联立直线与抛物线方程,根据方程组只有一解,得到k值,进而求出A,B两点坐标,代入直线斜率公式,可得答案.
解答:
解:设过(-3,2)与抛物线y2=12x相切的直线方程为:y-2=k(x+3),设点A(x1,y1),B(x2,y2).
由
得:y2-
y+
+36=0,
由△=
-
-144=0得:
k=-
,或k=
,
∴y1=-2(
-1),y2=2(
+1),
∴x1=
,x2=
,
则直线AB的斜率kAB=
=3
由
|
| 12 |
| k |
| 24 |
| k |
由△=
| 144 |
| k2 |
| 96 |
| k |
k=-
| ||
| 3 |
| ||
| 3 |
∴y1=-2(
| 10 |
| 10 |
∴x1=
11-2
| ||
| 3 |
11+2
| ||
| 3 |
则直线AB的斜率kAB=
| y1-y2 |
| x1-x2 |
点评:本题考查的知识点是直线与圆锥曲线的位置关系,本题计算量较大,要注意小心计算,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=sin(2x+
),g(x)=sin(2x-
),下列说法正确的是( )
| π |
| 3 |
| π |
| 3 |
A、f(x)的图象可以由g(x)的图象向左平移
| ||
B、f(x)的图象可以由g(x)的图象向右平移
| ||
C、f(x)的图象可以由g(x)的图象关于直线x=
| ||
D、f(x)的图象可以由g(x)的图象关于直线x=
|
某市缺水问题比较突出,为了制定水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x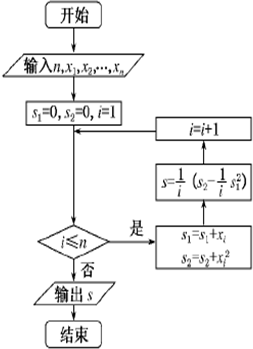 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知x,y为正实数,则下列各关系式正确的是( )
| A、2lgx+lgy=2lgx+2lgy |
| B、2lg(x+y)=2lgx•2lgy |
| C、2lgx•lgy=2lgx+2lgy |
| D、2lg(xy)=2lgx•2lgy |
 某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是
某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是