题目内容
已知A，B∈（0，
），且sinAcosB=3cosAsinB，tanA+tanB=7-tanAtanB．
（1）求∠B的值；
（2）求
的值．
| π |
| 2 |
（1）求∠B的值；
（2）求
| sinAsinB-cosAcosB |
| sinAsinB+2cosAcosB |
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：（1）由已知可得tanA=3tanB．又由tanA+tanB=7-tanAtanB得4tanB=7-3tan2B，从而可求B的值；
（2）由（1）得：tanB=1，tanA=3，又由A，B∈（0，
），即可求值．
（2）由（1）得：tanB=1，tanA=3，又由A，B∈（0，
| π |
| 2 |
解答：
解：（1）∵sinAcosB=3cosAsinB，∴可得tanA=3tanB．
∵tanA+tanB=7-tanAtanB．∴4tanB=7-3tan2B
∴可解得：tanB=1或-
∵B∈（0，
），tanB＞0
∴tanB=1
∴∠B=
．
（2）∵由（1）得：tanB=1，tanA=3
又∵A，B∈（0，
），
∴
=
=
．
∵tanA+tanB=7-tanAtanB．∴4tanB=7-3tan2B
∴可解得：tanB=1或-
| 14 |
| 6 |
∵B∈（0，
| π |
| 2 |
∴tanB=1
∴∠B=
| π |
| 4 |
（2）∵由（1）得：tanB=1，tanA=3
又∵A，B∈（0，
| π |
| 2 |
∴
| sinAsinB-cosAcosB |
| sinAsinB+2cosAcosB |
| tanAtanB-1 |
| tanAtanB+2 |
| 2 |
| 5 |
点评：本题主要考察了同角三角函数基本关系的运用，属于基本知识的考查．
练习册系列答案
相关题目
已知sinα-cosα=
，则tanα+
=（ ）
| 1 |
| 3 |
| 1 |
| tanα |
A、
| ||
B、
| ||
C、
| ||
D、
|
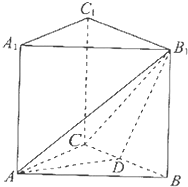如图，在棱长均相等的正三棱柱ABC-A1B1C1中，D为BC的中点．
如图，椭圆C：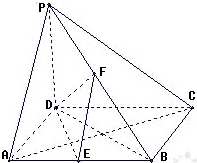
已知四棱锥P-ABCD，底面是边长为a的正方形，PD⊥底面ABCD，PD=DC，E、F分别是AB、PB的中点，