题目内容
9．已知命题p：x2-5x-6≤0，命题q：x2-2x+1-4a2≤0（a＞0），若￢p是￢q的必要不充分条件，求实数a的取值范围．分析 求出命题的等价条件，结合充分条件和必要条件的关系进行转化求解即可．
解答 解：因为x2-5x-6≤0，所以（x-6）（x+1）≤0，
所以p：-1≤x≤6，…..（2分）
因为x2-2x+1-4a2≤0（a＞0），
所以[x-（1+2a）][x-（1-2a）]≤0，…..（4分）
又a＞0，所以q：1-2a≤x≤1+2a，
因为?p是?q的必要不充分条件，
所以q是p的必要不充分条件，…..（6分）
所以$\left\{\begin{array}{l}1+2a≥6\\ 1-2a≤-1\\ a＞0\end{array}\right.∴a≥\frac{5}{2}$，经验证$，a≥\frac{5}{2}$符合题意．
故a的取值范围为$[\frac{5}{2}，+∞）$…．（12分）
点评 本题主要考查充分条件和必要条件的应用，求出命题的等价条件结合逆否命题的等价性是解决本题的关键．
练习册系列答案
相关题目
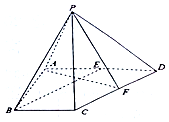如图，在四棱锥P-ABCD中，△PCD为等边三角形，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD=2BC=2，AB=$\sqrt{3}$，点E、F分别为AD、CD的中点．
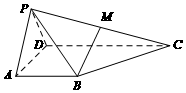在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为等边三角形，$AB=AD=\frac{1}{2}CD$，AB⊥AD，AB∥CD，点M是PC的中点．
1．已知$tanθ=\frac{1}{2}$，则$tan（{\frac{π}{4}-2θ}）$=（ ）
| A． | 7 | B． | -7 | C． | $\frac{1}{7}$ | D． | $-\frac{1}{7}$ |
18．在△ABC中，若BC=2，A=120°，则$\overrightarrow{AB}$•$\overrightarrow{CA}$的最大值为（ ）
| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | -$\frac{4}{3}$ |