题目内容
4.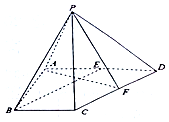 如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.
如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.(1)求证:直线BE∥平面PCD;
(2)求证:平面PAF⊥平面PCD;
(3)若PB=$\sqrt{3}$,求直线PB与平面PAF所成的角.
分析 (1)推导出四边形BCDE是平行四边形,从而BE∥CD,由此能证明直线BE∥平面PCD.
(2)推导出CD⊥PF,AB⊥BC,CD⊥AF,从而CD⊥平面PAF,由此能证明平面PAF⊥平面PCD.
(3)设AF与BE交于点G,连结PG,则∠BPG为直线BP与平面PAF所成的角,由此能求出直线PB与平面PAF所成的角.
解答 (本小题满分13分)
证明:(1)∵AD=2BC=2,且E为AD的中点,∴BC=ED.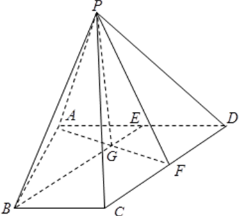
又因为AD∥BC,则四边形BCDE是平行四边形,∴BE∥CD,
∵CD?平面PCD,BE?平面PCD,
∴直线BE∥平面PCD.…(4分)
(2)∵在等边△PCD中,F是CD的中点,∴CD⊥PF,
又BC∥AD,AB⊥AD,∴AB⊥BC,
又$AB=\sqrt{3},BC=1$,∴AC=2,
又AD=2,∴CD⊥AF,又∵PF∩AF=F,∴CD⊥平面PAF,
故平面PAF⊥平面PCD.…(8分)
解:(3)设AF与BE交于点G,
由(2)知CD⊥平面PAF,BE∥CD,
故BG⊥平面PAF,连结PG,
则∠BPG为直线BP与平面PAF所成的角.
在Rt△PBG中,$BG=\frac{3}{2}$,$sin∠BPG=\frac{BG}{PB}=\frac{{\frac{3}{2}}}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{2}$,
∴$∠BPG=\frac{π}{3}$.
∴直线PB与平面PAF所成的角$\frac{π}{3}$.…(13分)
点评 本题考查面面平行的证明,考查面面垂直的证明,考查线面角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
14.过点A(3,5)作圆(x-2)2+(y-3)2=1的切线,则切线的方程为( )
| A. | x=3或3x+4y-29=0 | B. | y=3或3x+4y-29=0 | C. | x=3或3x-4y+11=0 | D. | y=3或3x-4y+11=0 |
15.已知f(x)=(x2-3)ex(其中x∈R,e是自然对数的底数),当t1>0时,关于x的方程[f(x)-t1][f(x)-t2]=0恰好有5个实数根,则实数t2的取值范围是( )
| A. | (-2e,0) | B. | (-2e,0] | C. | [-2e,6e-3] | D. | (-2e,6e-3) |
12.已知$a={log_3}0.5,b={log_{0.3}}0.2,c={0.5^{0.3}}$,则( )
| A. | a>c>b | B. | b>c>a | C. | b>a>c | D. | c>a>b |
13.等比数列{an}中,a2+a4=20,a3+a5=40,则a6=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |