题目内容
将-330°化为弧度为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
考点:弧度与角度的互化
专题:三角函数的求值
分析:设-330°=x弧度,则
=
,解方程可得.
| 180 |
| -330 |
| π |
| x |
解答:
解:∵180°=π弧度,
设-330°=x弧度,
则有
=
,
解得x=-
=-
,
∴-330°=-
弧度
故选:B
设-330°=x弧度,
则有
| 180 |
| -330 |
| π |
| x |
解得x=-
| 330π |
| 180 |
| 11π |
| 6 |
∴-330°=-
| 11π |
| 6 |
故选:B
点评:本题考查角度与弧度的转化,由180°=π弧度入手建立比例式是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
物体自由落体运动方程为s(t)=
gt2,若
=g=9.8m/s,那么下面说法正确的是( )
| 1 |
| 2 |
| lim |
| n→∞ |
| s(1+△t)-s(1) |
| △t |
| A、9.8m/s是0~1s这段时间内的平均速度 |
| B、9.8m/s是从1s到(1+△t)s这段时间内的速度 |
| C、9.8m/s是物体在t=1s这一时刻的速度 |
| D、9.8m/s是物体从1s到(1+△t)s这段时间内的平均速度 |
如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
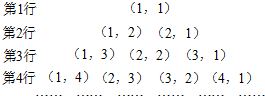 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.