题目内容
19.若$\overrightarrow{a}$为非零向量,且$\overrightarrow{b}$=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$,$\overrightarrow{c}$=(cosθ,sinθ),则向量$\overrightarrow{b}$与$\overrightarrow{c}$一定满足( )| A. | $\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | ($\overrightarrow{b}$+$\overrightarrow{c}$)⊥($\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{a}$ | D. | $\overrightarrow{b}$•$\overrightarrow{c}$=0 |
分析 由题意可知|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,于是($\overrightarrow{b}$+$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=${\overrightarrow{b}}^{2}$-${\overrightarrow{c}}^{2}$=0.
解答 解:∵$\overrightarrow{b}$=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$.∴$\overrightarrow{b}$为与$\overrightarrow{a}$同向的单位向量,
又∵$\overrightarrow{c}$=(cosθ,sinθ),∴|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,
∴($\overrightarrow{b}$+$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=${\overrightarrow{b}}^{2}$-${\overrightarrow{c}}^{2}$=1-1=0,
∴($\overrightarrow{b}$+$\overrightarrow{c}$)⊥($\overrightarrow{b}$-$\overrightarrow{c}$).
故选:B.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
9.已知直线l是曲线C1:y=x2与曲线C2:y=lnx,x∈(0,1)的一条公切线,若直线l与曲线C1的切点为P,则点P的横坐标t满足( )
| A. | 0<t<$\frac{1}{2}$ | B. | $\frac{1}{2}$<t<1 | C. | $\frac{\sqrt{2}}{2}$<t<$\sqrt{2}$ | D. | $\sqrt{2}$<t<$\sqrt{3}$ |
14.已知变量x,y满足线性约束条件$\left\{\begin{array}{l}{x+y+1≥0}\\{x-y+2≥0}\\{3x+y-2≤0}\end{array}\right.$,若目标函数z=ax-y仅在点(0,2)处取得最小值,则实数a的取值范围是( )
| A. | (-∞,-3) | B. | (3,+∞) | C. | (-3,1) | D. | (-1,1) |
11.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|x2-1<0},则A∩B=( )
| A. | ∅ | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|0<x<1} |
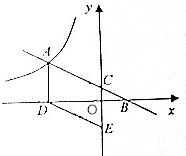 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.