题目内容
2.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量,非零向量$\overrightarrow{b}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,x,y∈R,若x+2y=2,则|$\overrightarrow{b}$|的最小值为1.分析 计算${\overrightarrow{b}}^{2}$,将x=2-2y代入得到关于y的函数,求此函数的最小值.
解答 解:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=cos$\frac{π}{3}$=$\frac{1}{2}$.$\overrightarrow{b}$2=x2+y2+2xy$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=x2+y2+xy.
∵x+2y=2,∴x=2-2y.
∴$\overrightarrow{b}$2=(2-2y)2+y2+(2-2y)y=3y2-6y+4=3(y-1)2+1.
∴当y=1时,$\overrightarrow{b}$2取得最小值1.
∴|$\overrightarrow{b}$|的最小值为1.
故答案为:1.
点评 本题考查了平面向量数量积的运算,二次函数的最值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若方程E:$\frac{x^2}{1-m}-\frac{y^2}{m-2}$=1表示焦点在y轴上的双曲线,则实数m的取值范围为( )
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-∞,2) | D. | (1,+∞) |
13.过点$P(-\sqrt{3},-1)$的直线l与圆x2+y2=1有公共点,则直线l的斜率的取值范围是( )
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\sqrt{3}]$ | C. | $[0,\frac{{\sqrt{3}}}{3}]$ | D. | $[0,\sqrt{3}]$ |
12. 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
(I)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表参考公式:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):(I)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
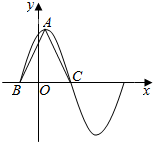 函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.