题目内容
12. 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):(I)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)由频率分布直方图可得,损失不少于6000元的居民共有(0.00003+0.00003)×2000×50=6户,损失为6000~8000元的居民共有0.00003×2000×50=3户,损失不少于8000元的居民共有0.00003×2000×50=3户,即可求这两户在同一分组的概率;
(Ⅱ)求出K2,与临界值比较,即可得出结论.
解答 解:(I)由频率分布直方图可得,损失不少于6000元的居民共有(0.00003+0.00003)×2000×50=6户,
损失为6000~8000元的居民共有0.00003×2000×50=3户,
损失不少于8000元的居民共有0.00003×2000×50=3户,…(3分)
因此,这两户在同一分组的概率为 P=$\frac{{C}_{3}^{2}+{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$ …(6分)
(II)如表:
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
K2=$\frac{50×(30×6-9×5)^{2}}{39×11×35×15}$…(8分)
=$\frac{4050}{1001}$=4.046>3.841…(10分)
所以有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否4000元有关.…(12分)
点评 本题考查频率分布直方图,独立性检验知识,考查古典概型,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
相关题目
17.为了帮家里减轻负担,高二学生小明利用暑假时间打零工赚学费.他统计了其中五天的工作时间x(小时)与报酬y(元)的数据,分别是(2,30),(4,40),(5,m),(6,50),(8,70),他用最小二乘法得出y与x的线性回归方程为y=6.5x+17.5,则其中m为( )
| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
1.已知a>0,b>0满足a+b=2,则$\frac{1}{a}+\frac{9}{b}$的最小值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 24 |
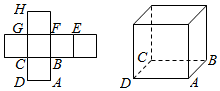 一个正方体的平面展开图及正方体的直观图的示意图如图所示:
一个正方体的平面展开图及正方体的直观图的示意图如图所示: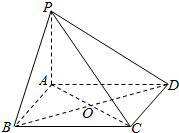 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.