题目内容
13.过点$P(-\sqrt{3},-1)$的直线l与圆x2+y2=1有公共点,则直线l的斜率的取值范围是( )| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\sqrt{3}]$ | C. | $[0,\frac{{\sqrt{3}}}{3}]$ | D. | $[0,\sqrt{3}]$ |
分析 用点斜式设出直线方程,根据直线和圆有交点、圆心到直线的距离小于或等于半径可得$\frac{|0-0+\sqrt{3}k-1|}{\sqrt{{k}^{2}+1}}$≤1,由此求得斜率k的范围.
解答 解:由题意可得点$P(-\sqrt{3},-1)$在圆x2+y2=1的外部,故要求的直线的斜率一定存在,设为k,
则直线方程为y+1=k(x+$\sqrt{3}$),即 kx-y+$\sqrt{3}$k-1=0.
根据直线和圆有公共点、圆心到直线的距离小于或等于半径可得$\frac{|0-0+\sqrt{3}k-1|}{\sqrt{{k}^{2}+1}}$≤1,
即3k2-2$\sqrt{3}$k+1≤k2+1,解得0≤k≤$\sqrt{3}$,
故选:D.
点评 本题主要考查用点斜式求直线方程,点到直线的距离公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
1.给定函数①y=x${\;}^{\frac{1}{2}}$②y=log${\;}_{\frac{1}{2}}$(x+1)③y=|x2-2x|④y=($\frac{5}{6}$)x,其中在区间(0,1)上单调递减的函数序号是( )
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ①③ |
18.已知α∈(0,$\frac{π}{2}$),且cos(α+$\frac{π}{3}$)=-$\frac{3}{5}$,则sinα的值为( )
| A. | $\frac{3-4\sqrt{3}}{10}$ | B. | $\frac{3+4\sqrt{3}}{10}$ | C. | $\frac{4-3\sqrt{3}}{10}$ | D. | $\frac{4+3\sqrt{3}}{10}$ |
5.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-4x+5 | B. | y=9-x2 | C. | y=($\frac{1}{2}$)x | D. | y=|x| |
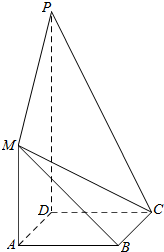 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.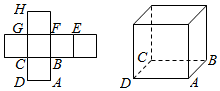 一个正方体的平面展开图及正方体的直观图的示意图如图所示:
一个正方体的平面展开图及正方体的直观图的示意图如图所示: