若方程E:$\frac{x^2}{1-m}-\frac{y^2}{m-2}$=1表示焦点在y轴上的双曲线.则实数m的取值范围为( )A．(1.2)B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

12．若方程E：$\frac{x^2}{1-m}-\frac{y^2}{m-2}$=1表示焦点在y轴上的双曲线，则实数m的取值范围为（　　）

A．

（1，2）

B．

（-∞，1）∪（2，+∞）

C．

（-∞，2）

D．

（1，+∞）

分析利用双曲线的性质直接求解．

解答解：∵方程E：$\frac{x^2}{1-m}-\frac{y^2}{m-2}$=1表示焦点在y轴上的双曲线，
∴$\left\{\begin{array}{l}{1-m＜0}\\{m-2＜0}\end{array}\right.$，解得1＜m＜2．
∴实数m的取值范围为（1，2）．
故选：A．

点评本题考查实数的取值范围的求法，是基础题，解题时要认真审题，注意双曲线性质的合理运用．

练习册系列答案

18．（1）求正整数列前n个偶数的和；
（2）求正整数列前n个奇数的和；
（3）在三位正整数的集合中有多少个数是5的倍数？求它们的和．
（4）在正整数集合中有多少个三位数？求它们的和．

15．S_n是数列{a_n}的前n项和，且a₁=1，a_n+1=2a_n+n-1，S₁₀=1991．

7．

如图的几何体中，AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．
（1）求证：AF∥平面BCE；
（2）求证：平面BCE⊥平面CDE．

17．设数列{a_n}的前n项和为S_n，且a₁=-1，a_n+1=S_n•S_n+1，则数列{a_n}的通项公式a_n=$\left\{\begin{array}{l}{-1，n=1}\\{\frac{1}{n（n-1）}，n≥2}\end{array}\right.$．

4．

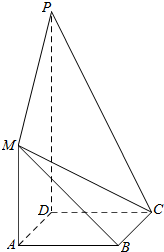如图，正方形ABCD与梯形AMPD所在的平面互相垂直，AD⊥PD，MA∥PD，MA=AD=$\frac{1}{2}$PD=1．
（Ⅰ）求证：MB∥平面PDC；
（Ⅱ）求二面角M-PC-D的余弦值；
（Ⅲ）E为线段PC上一点，若直线DE与直线PM所成的角为60°，求PE的长．

1．给定函数①y=x${\;}^{\frac{1}{2}}$②y=log${\;}_{\frac{1}{2}}$（x+1）③y=|x²-2x|④y=（$\frac{5}{6}$）^x，其中在区间（0，1）上单调递减的函数序号是（　　）

2．已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量，非零向量$\overrightarrow{b}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，x，y∈R，若x+2y=2，则|$\overrightarrow{b}$|的最小值为1．

试题分类