题目内容

在△ABC中，a，b，c分别是内角A，B，C所对的边，若b=5，B=
π
4
，tanA=2，则sinA=
 
；a=
 
．
考点：正弦定理,同角三角函数间的基本关系
专题：解三角形
分析：由条件利用同角三角函数的基本关系、正弦定理，求得sinA和a的值．
解答： 解：在△ABC中，∵tanA=2=
sinA
cosA
，sin2A+cos2A=1，可得sinA=
2
5
5
，cosA=
5
5
．
再根据b=5，B=
π
4
，由正弦定理可得
a
sinA
=
b
sinB
，即
a
2
5
5
=
5
2
2
，求得a=2
10
，
故答案为：
2
5
5
；2
10
．
点评：本题主要考查同角三角函数的基本关系、正弦定理的应用，属于基础题．
练习册系列答案
相关题目
①正相关，②负相关，③不相关，则下列散点图分别反映的变量是（　　）
A、①②③B、②③①
C、②①③D、①③②
已知在区间[-1，1]上随机地取一个数x，则-π（x2-1）的值介于
8π
9
到π之间的概率为（　　）
A、
1
3
B、
2
π
C、
1
2
D、
2
3
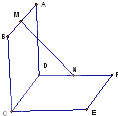如图，已知两个正方形ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点．若平面ABCD⊥平面DCEF，求直线MN与平面DCEF所成角的正弦值．
已知圆C：x2+y2-2x-4y+m=0．
（1）求m的取值范围．
（2）当m=4时，若圆C与直线x+ay-4=0交于M，N两点，且
CM
⊥
CN
，求a的值．
已知空间中三点A（-2，0，2），B（-1，1，2），C（-3，0，4），设
AB
=
a
，
AC
=
b
．
（1）若|
c
|=3，且
c
∥
BC
，求
c
；
（2）求
a
与
b
的夹角的余弦值；
（3）若k
a
+
b
与k
a
-2
b
互相垂直，求实数k的值．
命题p：关于x的不等式x2+（a-1）x+a2≤0的解集为∅；命题q：函数y=（2a2-a）x为增函数． 分别求出符合下列条件的实数a的取值范围．
（1）p、q至少有一个是真命题；
（2）p或q是真命题且p且q是假命题．
下列命题中正确的有
 
  （填写正确的序号）
（1）已知f（n）=sin
nπ
6
，则f（1）+f（2）+…+f（2014）=1；
（2）已知向量
OA
=（0，1），
OB
=（k，k），
OC
=（1，3），且
AB
∥
AC
，则实数k=-1；
（3）四位二进制数能表示的最大十进制数是15；
（4）函数y=cos（2x+
π
3
）的图象的一个对称中心是（
π
12
，0）
（5）若对任意实数a，函数y=5sin（
2k+1
3
πx-
π
6
）（k∈N）在区间[a，a+3]上的值
5
4
出现不少于4次且不多于8次，则k的值是2．
将函数y=3sin（2x-
π
4
）的图象经过（　　）变换，可以得到函数y=3sin2x的图象．
A、沿x轴向右平移
π
8
个单位
B、沿x轴向左平移
π
8
个单位
C、沿x轴向右平移
π
4
个单位
D、沿x轴向左平移
π
4
个单位

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网