题目内容
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
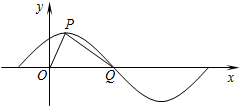
)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点,若OQ=4,OP=
,PQ=
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,当x∈(-1,2)时,求函数h(x)=f(x)•g(x)的值域.
| π |
| 2 |
| 5 |
| 13 |
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,当x∈(-1,2)时,求函数h(x)=f(x)•g(x)的值域.

考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)由条件利用余弦定理求得cos∠POQ的值,可得点P的坐标由此求得A的值,再根据点Q的坐标,由周期求得ω,再根据五点法作图求得φ的值,可得函数的解析式.
(Ⅱ)由条件利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)=2sin
x,利用三角恒等变换求得h(x)=1+2sin(
x-
),再利用正弦函数的定义域和值域,求得h(x)的值域.
(Ⅱ)由条件利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)=2sin
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
解答:
解:(Ⅰ)由函数y=f(x)的图象,OQ=4,OP=
,PQ=
,利用余弦定理可得cos∠POQ=
=
,
∴sin∠POQ=
=
,故点P(1,2),点Q(4,0),故有A=
.
再根据
•
=4-1=3,∴ω=
.
由五点法作图可得
•1+φ=
,求得φ=
,故函数的解析式为f(x)=2sin(
x+
).
(Ⅱ)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)=2sin[
(x-2)+
]=2sin
x的图象,
可得h(x)=f(x)•g(x)=2sin(
x+
)•2sin
x=4(sin
xcos
+cos
xsin
)sin
x=2sin2
x+2
sin
x•cos
x
=1-cos
x+
sin
x=1+2sin(
x-
).
当x∈(-1,2)时,
x-
∈(-
,
),sin(
x-
)∈(-1,1),y∈(-1,3).
| 5 |
| 13 |
| OP2+OQ2-PQ2 |
| 2OP•OQ |
| ||
| 5 |
∴sin∠POQ=
| 1-cos2∠POQ |
2
| ||
| 5 |
8
| ||
| 5 |
再根据
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 6 |
由五点法作图可得
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
(Ⅱ)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)=2sin[
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
可得h(x)=f(x)•g(x)=2sin(
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| π |
| 6 |
=1-cos
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
当x∈(-1,2)时,
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查余弦定理、由函数y=Asin(ωx+φ)的部分图象求解析式、函数y=Asin(ωx+φ)的图象变换规律、三角恒等变换、正弦函数的定义域和值域,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
将f(x)=cosx向右平移
个单位,得到函数y=g(x)的图象,则g(
)=( )
| π |
| 6 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|


 在一次“爱眼日”活动中,随机抽取高三(1)班6名男生和6名女生的视力数据制成茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶):视力为5.0(含5.0)以上为正常视力,其他为近视眼.
在一次“爱眼日”活动中,随机抽取高三(1)班6名男生和6名女生的视力数据制成茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶):视力为5.0(含5.0)以上为正常视力,其他为近视眼.