题目内容
从某大学中随机选取7名女大学生,其身高x(单位:cm)和体重y(单位:kg)数据如表:
(1)求根据女大学生的身高x预报体重y的回归方程;
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重;
(3)试分析说明回归方程预报的效果.
附:1.回归直线的斜率和截距的最小二乘法估计公式分别为:
=
,
=
-
.
2.反映回归效果的公式为:R2=1-
,其中R2越接近于1,表示回归的效果越好.
3.参考数据:
(y1-
)2=2.25.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 身高x | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
| 体重y | 52 | 52 | 53 | 55 | 54 | 56 | 56 |
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重;
(3)试分析说明回归方程预报的效果.
附:1.回归直线的斜率和截距的最小二乘法估计公式分别为:
 |
| b |
| ||||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
2.反映回归效果的公式为:R2=1-
| ||||||||
|
3.参考数据:
| ||
| i=1 |
 |
| yi |
考点:线性回归方程
专题:应用题,概率与统计
分析:(1)计算平均数,求出b,a,即可求出回归方程;
(2)b>0,可得这7名女大学生的身高和体重的变化具有正的线性相关关系,代入公式,预报一名身高为172cm的女大学生的体重;
(3)求出R2=1-
=87.5%,即可说明回归方程预报的效果.
(2)b>0,可得这7名女大学生的身高和体重的变化具有正的线性相关关系,代入公式,预报一名身高为172cm的女大学生的体重;
(3)求出R2=1-
| 2.25 |
| (4+4+1)×2 |
解答:
解:(1)∵
=
=166,
=
=54,
∴b=
=
,
∴a=54-
×166=-70.5,
∴y=
x-70.5;
(2)∵b>0,
∴这7名女大学生的身高和体重的变化具有正的线性相关关系,
x=172时,y=
×172-70.5=58.5(kg);
(3)R2=1-
=87.5%,
∴女大学生的体重差异有87.5%是由身高引起的,这说明回归方程预报的效果是良好的.
. |
| x |
| 163+164+165+166+167+168+169 |
| 7 |
. |
| y |
| 52+52+53+55+54+56+56 |
| 7 |
∴b=
| 6+4+1+0+0+4+6 |
| (9+4+1)×2 |
| 3 |
| 4 |
∴a=54-
| 3 |
| 4 |
∴y=
| 3 |
| 4 |
(2)∵b>0,
∴这7名女大学生的身高和体重的变化具有正的线性相关关系,
x=172时,y=
| 3 |
| 4 |
(3)R2=1-
| 2.25 |
| (4+4+1)×2 |
∴女大学生的体重差异有87.5%是由身高引起的,这说明回归方程预报的效果是良好的.
点评:本题考查回归方程,考查学生的计算能力,正确求出回归方程是关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则复数z所对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
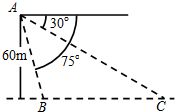 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )A、30(
| ||
B、120(
| ||
C、180(
| ||
D、240(
|
已知关于x的方程|x2-2x|=a(a>0)的解集为P,则P中所有元素的和可能是( )
| A、1,2,3 |
| B、2,3,4 |
| C、3,4,5 |
| D、2,3,5 |