题目内容
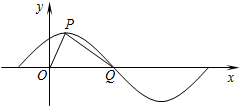
已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，在（0，+∞）上单调递减，且f（2）=0，若f（x-1）≤0，则x的取值范围为 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系先求出f（x）≤0解，即可得到结论．
解答：
解：∵奇函数f（x）在（0，+∞）上为减函数，且f（2）=0，
∴函数f（x）在（-∞，0）上为减函数，且f（-2）=f（2）=0，
作出函数f（x）的草图如图：在
则f（x）≤0的解为x≥2或-2≤x＜0，
由x-1≥2或-2≤x-1＜0，
得x≥3或-1≤x＜1，
故不等式f（x-1）≤0的解集是[-1，1）∪[3，+∞），
故答案为：[-1，1）∪[3，+∞）
解：∵奇函数f（x）在（0，+∞）上为减函数，且f（2）=0，∴函数f（x）在（-∞，0）上为减函数，且f（-2）=f（2）=0，
作出函数f（x）的草图如图：在
则f（x）≤0的解为x≥2或-2≤x＜0，
由x-1≥2或-2≤x-1＜0，
得x≥3或-1≤x＜1，
故不等式f（x-1）≤0的解集是[-1，1）∪[3，+∞），
故答案为：[-1，1）∪[3，+∞）
点评：本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
已知tanθ=2，则2sin2θ+sinθcosθ-cos2θ=（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的左、右焦点分别为F1，F2，P为双曲线上任一点，且
•
最小值的取值范围是[-
c2，-
c2]，则该双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 3 |
| 4 |
| 1 |
| 2 |
A、(1，
| ||
B、[
| ||
C、(1，
| ||
| D、[2，+∞） |
已知i是虚数单位，则
=（ ）
| i |
| 1-i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|