题目内容
已知x1,x2是方程x2-(k-2)+(k2+3k+5)=0(k∈R)的两个实根,则x12+x22的最大值为( )
| A、18 | ||
| B、19 | ||
C、5
| ||
| D、不存在 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:x1,x2是方程x2-(k-2)+(k2+3k+5)=0(k∈R)的两个实根,可得△≥0,解得-4≤k≤-
.再利用根与系数的关系、二次函数的单调性即可得出.
| 4 |
| 3 |
解答:
解:∵x1,x2是方程x2-(k-2)+(k2+3k+5)=0(k∈R)的两个实根,
∴△=(k-2)2-4(k2+3k+5)≥0,解得-4≤k≤-
.
∴x1+x2=k-2,x1•x2=k2+3k+5.
∴x12+x22=(x1+x2)2-2x1x2=(k-2)2-2(k2+3k+5)=-(k+5)2+19≤-(-4+5)2+19=18.
故选:A.
∴△=(k-2)2-4(k2+3k+5)≥0,解得-4≤k≤-
| 4 |
| 3 |
∴x1+x2=k-2,x1•x2=k2+3k+5.
∴x12+x22=(x1+x2)2-2x1x2=(k-2)2-2(k2+3k+5)=-(k+5)2+19≤-(-4+5)2+19=18.
故选:A.
点评:本题考查了一元二次方程的实数根与判别式的关系、根与系数的关系、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
复数z满足(z+i)•i=1+i(i是虚数单位),则复数z的模为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
若M={x|-2≤x<2},N={x|y=log2(x-1)},则M∩N=( )
| A、{x|-2≤x<0} |
| B、{x|-1<x<0} |
| C、{-2,0} |
| D、{x|1<x<2} |
 如图,F1,F2是分别是双曲线
如图,F1,F2是分别是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
双曲线x2-y2=2的离心率是( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
设0<a<1,关于x的不等式a (t2-1)x2-(t-1)x-1>1的解集为R,则实数t的取值范围是( )
A、(-
| ||
| B、(-1,1) | ||
C、(-
| ||
| D、[-1,1] |
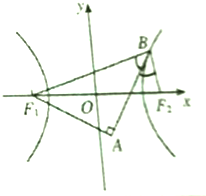 如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(
如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(