题目内容

已知向量
a
=（x1，y1），
b
=（x2，y2），且b≠0，给出以下结论
（1）
a
=λ
b
（λ∈R，且λ≠0）；（2）x1y1-x2y2=0；（3）x1y2-x2y1=0；（4）
x1
y1
-
x2
y2
=0； （5）
y2
x2
-
y1
x1
=0
则在以上各结论中能推导出
a
∥
b
，但由
a
∥
b
却推不出该结论的是
 
（填序号）
考点：命题的真假判断与应用,平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：利用向量共线的充要条件判断即可．
解答： 解：平面向量共线的充要条件：
a
∥
b
?
a
=λ
b
（λ∈R，且λ≠0；
向量
a
=（x1，y1），
b
=（x2，y2），
a
∥
b
?x1y2-x2y1=0．
所以
x1
y1
-
x2
y2
=0；可得x1y2-x2y1=0．得到
a
∥
b
．所以（4）正确；
y2
x2
-
y1
x1
=0，可得x1y2-x2y1=0．得到
a
∥
b
．所以（5）正确；
故答案为：（4）（5）．
点评：本题考查向量共线的充要条件判断与应用，基本知识的考查．
练习册系列答案
相关题目
“θ=-
π
3
”是“tanθ=2cos（
π
2
-θ）”的
 
条件．
复数z满足（z+i）•i=1+i（i是虚数单位），则复数z的模为（　　）
A、1
B、
3
C、
5
D、3
已知函数f（x）=
1
4x+2
，若函数y=f(x+
1
2
)+n为奇函数，则实数n等于（　　）
A、
1
4
B、0
C、-
1
4
D、-
1
2
下列集合表示法正确的是（　　）
A、{1，1，2}
B、{全体正数}
C、{有理数}
D、不等式x2-5＞0的解集为{x2-5＞0}
已知向量
a
=（cos（-θ），sin（π+θ）），
b
=（cos（
π
2
-θ），sin（
π
2
-θ））．
（Ⅰ）求证
a
⊥
b
；
（Ⅱ）若存在不等于0的实数k和t，使
x
=
a
+（t2+3）
b
，
y
=-k
a
+t
b
满足
x
⊥
y
，试求此时
k+t2
t
的最小值．
若M={x|-2≤x＜2}，N={x|y=log2（x-1）}，则M∩N=（　　）
A、{x|-2≤x＜0}
B、{x|-1＜x＜0}
C、{-2，0}
D、{x|1＜x＜2}
已知实数a＞0，函数f（x）=
x(x-a)，(x≥0)
-
9
40
x(x-a)，(x＜0)

（1）若函数f（x）在区间（-b，b）（b＞0）上存在最小值，求b的取值范围
（2）对于函数f（x），若存在区间[m，n]（n＞m），使{y|y=f（x），x∈[m，n]}=[m，n]，求a的取值范围，并写出满足条件的所有区间[m，n]．
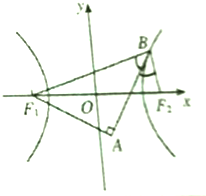如图，F1、F2分别是双曲线x2-y2=1的左右焦点，点A的坐标是（
2
2
，-
2
2
），点B在双曲线上，且
F1A
•
AB
=0
（1）求点B的坐标
（2）求证：∠F1BA=∠F2BA．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网