题目内容
解不等式:|x+1|-|x+2|≥3.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由原不等式可得①
,或②
,或 ③
.分别求得①、②、③的解集,再取并集,即得所求.
|
|
|
解答:
解:由不等式:|x+1|-|x+2|≥3.可得
①
,
或②
,
或③
.
解①求得x∈∅,解②求得x∈∅,解③求得x∈∅,
综上可得,原不等式的解集x∈∅,
故答案为:x∈∅.
①
|
或②
|
或③
|
解①求得x∈∅,解②求得x∈∅,解③求得x∈∅,
综上可得,原不等式的解集x∈∅,
故答案为:x∈∅.
点评:本题主要考查绝对值不等式的解法,体现了等价转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
已知A,B,C三点共线,{an}为等差数列,且
=a2
+a12
,则a3+a15-a11的值为( )
| OC |
| OA |
| OB |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
 如图,在边长为2正方形ABCD内作内切圆O,则将圆O绕对角线AC旋转一周得到的旋转体的表面积为( )
如图,在边长为2正方形ABCD内作内切圆O,则将圆O绕对角线AC旋转一周得到的旋转体的表面积为( )A、
| ||
| B、4 | ||
C、
| ||
| D、4π |
函数f(x)=2cos2x-sinx的最小值和最大值分别为( )
| A、-3,1 | ||
| B、-2,2 | ||
C、-3,
| ||
D、-2,
|
 已知椭圆E:
已知椭圆E: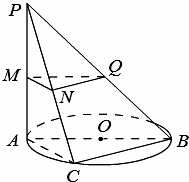 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.