题目内容
二阶矩阵M对应的变换将向量
,
分别变换成向量
,
,直线l在M的变换下所得到的直线l′的方程是2x-y-1=0,求直线l的方程.
|
|
|
|
考点:几种特殊的矩阵变换
专题:矩阵和变换
分析:根据定义直接计算即可.
解答:
解:设M=
,则由题知
=
,
=
,
所以
,解得
,
所以M=
.
设点P(x,y)是直线l上任一点,在M变换下对应的点为P′(x′,y′),
那么
=
,即
.
∵2x0-y0-1=0,
∴2(-x-4y)-(3x+5y)-1=0
即5x+13y+1=0,
因此直线l的方程是5x+13y+1=0.
|
|
|
|
|
|
|
所以
|
|
所以M=
|
设点P(x,y)是直线l上任一点,在M变换下对应的点为P′(x′,y′),
那么
|
|
|
|
∵2x0-y0-1=0,
∴2(-x-4y)-(3x+5y)-1=0
即5x+13y+1=0,
因此直线l的方程是5x+13y+1=0.
点评:本题考查矩阵与变换等基础知识与运算求解能力,属基础题.

练习册系列答案
相关题目
直线m与平面α平行的充要条件是( )
| A、直线m与平面α没有公共点 |
| B、直线m与平面α内的一条直线平行 |
| C、直线m与平面α内的无数条直线平行 |
| D、直线m与平面α内的任意一条直线平行 |
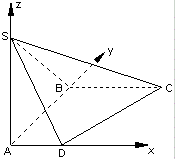 已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD= 如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.
如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.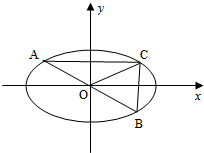 已知椭圆E:
已知椭圆E: