题目内容
设a，b，m为整数（m＞0），若a和b被m除得的余数相同，则称a和b对m同余记为a≡b（bmodm），已知a=1+C201+C2022+C20322+…+C2020219，a≡b（bmod10），则b的值可以是（ ）
| A、2015 | B、2013 |
| C、2011 | D、2009 |
考点：同余的性质（选修3）
专题：二项式定理
分析：根据已知中a和b对模m同余的定义，结合二项式定理，我们可以求出a的值，结合a≡b（bmod10），比照四个答案中的数字，结合得到答案．
解答：
解：∵a=1+C201+2C202+…+219C2020，（1+2）20=320=1+2C201+22C202+…+220C2020，
∴a=
．
∵31个位是3，32个位是9，33个位是7，34个位是1，35个位是3，…
∴320个位是1，
若a≡b（bmod10），则b的个位也是1．
故选C．
∴a=
| 320+1 |
| 2 |
∵31个位是3，32个位是9，33个位是7，34个位是1，35个位是3，…
∴320个位是1，
若a≡b（bmod10），则b的个位也是1．
故选C．
点评：本题考查同余定理，其中正确理解a和b对模m同余，是解答本题的关键，同时利用二项式定理求出a的值，也很关键．
练习册系列答案
阅读快车系列答案
相关题目
在区间（0，+∞）上不是增函数的函数是（ ）
| A、y=2-x | ||
| B、y=ln（x+1） | ||
C、y=-
| ||
| D、y=2x2+x+1 |
若直线y=kx-k交抛物线y2=4x于A，B两点，且线段AB中点到y轴的距离为3，则|AB|=（ ）
| A、12 | B、10 | C、8 | D、6 |
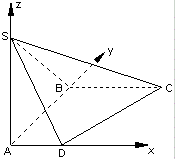已知ABCD是直角梯形，∠ABC=90°，SA⊥平面ABCD，SA=AB=BC=1，AD=
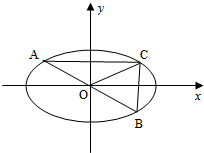已知椭圆E：