题目内容
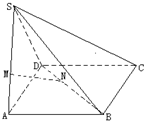 如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且
如图,已知S是平行四边形ABCD所在平面外一点,M,N分别是SA,BD上的点,MN=5,AB=AD=SB=SA=6,且| AM |
| SM |
| DN |
| NB |
| 1 |
| 2 |
(1)求MN与BC所成的角的余弦值;
(2)求证:MN∥平面SBC.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)在平面SAB中过点M作SB的平行线交AB于E,连接EN,说明∠MNE就是MN与BC所成的角,在MNE中,由余弦定理,求解cos∠MNE.
(2)证明ME∥平面SBC,EN∥平面SBC,推出平面MNE∥平面SBC.然后证明MN∥平面SBC.
(2)证明ME∥平面SBC,EN∥平面SBC,推出平面MNE∥平面SBC.然后证明MN∥平面SBC.
解答:
解:(1)在平面SAB中过点M作SB的平行线交AB于E,
连接EN,∴
=
,又
=
,∴EN∥AD,
所以∠MNE就是MN与BC所成的角.∵
=
=
,AB=AD=SB=SA=6,
∴在MNE中,MN=5,ME=2,NE=4,由余弦定理得cos∠MNE=
.
(2)由(1)知,ME∥SB,ME?平面SBC,SB?平面SBC,∴ME∥平面SBC,
∵EN∥AD,AD∥BC,∴EN∥BC,EN?平面SBC,BC?平面SBC,∴EN∥平面SBC,
∵EN?平面MNE,ME?平面MNE,EN∩ME=E,∴平面MNE∥平面SBC.
∵MN?平面MNE,MN∥平面SBC.
连接EN,∴
| AM |
| SM |
| AE |
| EB |
| AM |
| SM |
| DN |
| NB |
所以∠MNE就是MN与BC所成的角.∵
| AM |
| SM |
| DN |
| NB |
| 1 |
| 2 |
∴在MNE中,MN=5,ME=2,NE=4,由余弦定理得cos∠MNE=
| 37 |
| 40 |
(2)由(1)知,ME∥SB,ME?平面SBC,SB?平面SBC,∴ME∥平面SBC,
∵EN∥AD,AD∥BC,∴EN∥BC,EN?平面SBC,BC?平面SBC,∴EN∥平面SBC,
∵EN?平面MNE,ME?平面MNE,EN∩ME=E,∴平面MNE∥平面SBC.
∵MN?平面MNE,MN∥平面SBC.
点评:本题考查直线与平面平行的证明,平面与平面平行的性质定理,异面直线所成角的求法.考查空间想象能力以及计算能力、

练习册系列答案
相关题目
若集合M={y|y=2-x},N={x|y=
},则M∩N等于( )
| x-1 |
| A、{y|y>1} |
| B、{y|y≥1} |
| C、{y|y>0} |
| D、{y|y≥0} |
 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.