题目内容
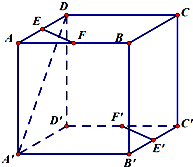 如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.
如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.(1)求证:EF
| ||
. |
(2)求直线A′D与EF所成角的大小.
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:计算题,空间位置关系与距离,空间角
分析:(1)利用三角形中位线的性质,结合BD
B′D′,可得结论;
(2)证明∠A′DB是直线A′D与EF所成角,可求直线A′D与EF所成角的大小.
| ||
. |
(2)证明∠A′DB是直线A′D与EF所成角,可求直线A′D与EF所成角的大小.
解答:
(1)证明:连接BD,B′D′,则,
∵E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点,
∴EF
BD,E′F′
B′D′,
∵BD
B′D′,
∴EF
E′F′;
(2)解:连接A′B,则
∵EF
BD,
∴∠A′DB是直线A′D与EF所成角,
∵△A′DB是等边三角形,
∴∠A′DB=60°,即直线A′D与EF所成角是60°.
∵E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点,
∴EF
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
∵BD
| ||
. |
∴EF
| ||
. |
(2)解:连接A′B,则
∵EF
| ||
. |
∴∠A′DB是直线A′D与EF所成角,
∵△A′DB是等边三角形,
∴∠A′DB=60°,即直线A′D与EF所成角是60°.
点评:本题考查直线与直线平行的证明,考查直线A′D与EF所成角,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
是( )
| |x| | ||
|
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数,又是偶函数 |
| D、既不是奇函数,也不是偶函数 |
若方程
=x(a∈R)在[-1,1]有解,则a的取值范围是( )
| 2x+x-a |
| A、[1,2] | ||
B、[-
| ||
| C、[1,3] | ||
D、[-
|
用秦九韶算法求当x=1.032时多项式f(x)=3x2+2x+3的值时,需要m次乘法运算,n次加法运算,m,n分别为( )
| A、3,2 | B、4,3 |
| C、2,2 | D、2,3 |
下列函数中,在R上是增函数的是( )
| A、y=-x+1 | ||
| B、y=-x2 | ||
C、y=
| ||
| D、y=x3 |