题目内容
解不等式:|x-5|-|2x-3|<1.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:分x≤
,
<x<5,x≥5三种情况进行讨论,去掉绝对值符号,解不等式即可求解,注意最后求并集.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:当x≤
时,原式即:5-x-(3-2x)<1,
解得:x<-1,则x的范围是:x<-1;
当
<x<5时,原式即5-x-(2x-3)<1,
解得:x>
,则x的范围是:
<x<5;
当x≥5时,原式即:x-5-(2x-3)<1,
解得:x>-3,则x的范围是:x≥5.
综上,x<-1或x>
.
故不等式的解集为(-∞,-1)∪(
,+∞).
| 3 |
| 2 |
解得:x<-1,则x的范围是:x<-1;
当
| 3 |
| 2 |
解得:x>
| 7 |
| 3 |
| 7 |
| 3 |
当x≥5时,原式即:x-5-(2x-3)<1,
解得:x>-3,则x的范围是:x≥5.
综上,x<-1或x>
| 7 |
| 3 |
故不等式的解集为(-∞,-1)∪(
| 7 |
| 3 |
点评:本题考查了含有绝对值的不等式的解法,正确对x的范围进行讨论,正确去掉绝对值符号是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若函数f(x)对任意a>0且a≠1,都有f(ax)=af(x),则称函数为“穿透”函数,则下列函数中,不是“穿透”函数的是( )
| A、f(x)=-x |
| B、f(x)=x+1 |
| C、f(x)=|x| |
| D、f(x)=x-|x| |
设直线l1、l2的方向向量分别为
=(0,-3,3),
=(-1,1,0),则直线l1、l2的夹角是( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
各棱长均为a的三棱锥的表面积为( )
A、4
| ||
B、3
| ||
C、2
| ||
D、
|
已知数列{an}的首项a1=2,且an+1=2an+1,(n≥1,n∈N+),则a5=( )
| A、7 | B、15 | C、30 | D、47 |
设l、m为两条直线,α为一个平面,下列四个命题中正确的是( )
| A、若l∥m,m?α,则l∥α |
| B、若l∥α,m?α,则l∥m |
| C、若l∥α,m?α,则l与m不平行 |
| D、若l∥m,l∥α,m?α,则m∥α |
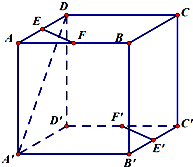 如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.
如图,在正方体AC′中,E,F,E′,F′分别是AD,AB,B′C′,D′C′的中点.