题目内容
6.用数归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,在第二步时,正确的设法是( )| A. | 设n=k(k∈N*)正确,再推n=k+1时正确 | |
| B. | 设n=k(k∈N*)正确,再推n=2k+1时正确 | |
| C. | 设n=k(k∈N*)正确,再推n=k+2时正确 | |
| D. | 设n=2k+1(k∈N*)正确,再推n=2k-1时正确 |
分析 根据连续正奇数的差为2得出正确选项.
解答 解:由于连续正奇数相差为2,故在假设n=k成立时,应推导n=k+2成立即可.
故选C.
点评 本题考查了数学归纳法的证明步骤,属于基础题.

练习册系列答案
相关题目
17.已知点A(0,1),B(3,2),向量$\overrightarrow{CA}=(4,3)$,则向量$\overrightarrow{BC}$=( )
| A. | (-7,-4) | B. | (7,4) | C. | (-1,4) | D. | (1,4) |
14.若角520°的始边为x轴非负半轴,则它的终边落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.下列命题正确的是( )
| A. | 若两个平面平行于同一条直线,则这两个平面平行 | |
| B. | 若有两条直线与两个平面都平行,则这两个平面平行 | |
| C. | 若有一条直线与两个平面都垂直,则这两个平面平行 | |
| D. | 若有一条直线与这两个平面所成的角相等,则这两个平面平行 |
18.已知tanθ=-$\frac{5}{12}$,θ∈($\frac{3π}{2}$,2π),则cos(θ+$\frac{π}{4}$)=( )
| A. | $\frac{{5\sqrt{2}}}{13}$ | B. | $\frac{{7\sqrt{2}}}{13}$ | C. | $\frac{{17\sqrt{2}}}{26}$ | D. | $\frac{{7\sqrt{2}}}{26}$ |
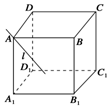 如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.
如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.