题目内容
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-
的解集是( )
| 1 |
| 2 |
| A、(-∞,-1] |
| B、(-∞,-1) |
| C、[1,+∞) |
| D、(1,+∞) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系,即可得到结论.
解答:
解:∵函数f(x)是定义在R上的奇函数,∴f(0)=0,不满足不等式f(x)<-
,
若x>0,由f(x)<-
得1-2-x<-
,
即2-x>
,此时不成立,
若x<0,则-x>0,此时f(-x)=1-2x=-f(x),
则f(x)=2x-1,
由f(x)<-
得2x-1<-
,
即2x<
,解得x<-1,
故不等式f(x)<-
的解集(-∞,-1),
故选:B
| 1 |
| 2 |
若x>0,由f(x)<-
| 1 |
| 2 |
| 1 |
| 2 |
即2-x>
| 3 |
| 2 |
若x<0,则-x>0,此时f(-x)=1-2x=-f(x),
则f(x)=2x-1,
由f(x)<-
| 1 |
| 2 |
| 1 |
| 2 |
即2x<
| 1 |
| 2 |
故不等式f(x)<-
| 1 |
| 2 |
故选:B
点评:本题主要考查不等式的求解,利用函数的奇偶性的性质求出函数的解析式是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知一个几何体的三视图及长度如图所示,则该几何体的体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知向量
=(1,2),
=(1+m,m-1),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
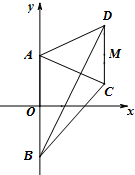 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=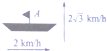 如图,一艘船从A点出发以2
如图,一艘船从A点出发以2