题目内容
若函数f(x)=e -(x-μ)2(e为无理数,e≈2.71828…)的最大值是m,且f(x)是偶函数,则m+μ= .
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:根据偶函数的性质和指数函数的图象和性质即可求出
解答:
解:∵函数f(x)=e -(x-μ)2是偶函数,
∴f(-x)=f(x),
∴(x-μ)2=(-x-μ)2,
解得μ=0,
∵函数f(x)=e-x2(e为无理数,e≈2.71828…)的最大值是m,
∴当x=0时,函数有最大值,f(x)max=f(0)=1=m,
∴m+μ=1,
故答案为:1
∴f(-x)=f(x),
∴(x-μ)2=(-x-μ)2,
解得μ=0,
∵函数f(x)=e-x2(e为无理数,e≈2.71828…)的最大值是m,
∴当x=0时,函数有最大值,f(x)max=f(0)=1=m,
∴m+μ=1,
故答案为:1
点评:本题主要考查了指数函数的图象和性质,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某三棱锥的三视图如图所示,这个三棱锥最长棱的棱长是( )


| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
若函数f(x)=x2-2x(x∈R),则f(x)的零点个数为( )个.
| A、1 | B、2 | C、3 | D、4 |
△ABC的内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且c=2a,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,M是BC的中点,AM=5,BC=6,则
•
等于( )
| AB |
| AC |
| A、9 | B、12 | C、16 | D、30 |
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-
的解集是( )
| 1 |
| 2 |
| A、(-∞,-1] |
| B、(-∞,-1) |
| C、[1,+∞) |
| D、(1,+∞) |
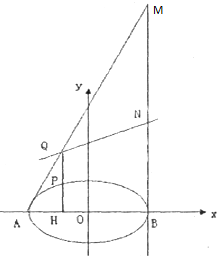 椭圆C:
椭圆C: