题目内容
1.若集合M={x∈N|x2-8x+7<0},N={x|$\frac{x}{3}$∉N},则M∩N等于( )| A. | {3,6} | B. | {4,5} | C. | {2,4,5} | D. | {2,4,5,7} |
分析 求解一元二次不等式化简M,再由交集运算得答案.
解答 解:∵M={x∈N|x2-8x+7<0}={x∈N|1<x<7}={2,3,4,5,6},N={x|$\frac{x}{3}$∉N},
∴M∩N={2,3,4,5,6}∩{x|$\frac{x}{3}$∉N}={2,4,5},
故选:C.
点评 本题考查交集及其运算,考查了一元二次不等式的解法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.集合A={$\frac{9}{10-x$∈N|x∈N}的真子集的个数是( )
| A. | 4 | B. | 7 | C. | 8 | D. | 16 |
9.设集合A={x|x≥2},B={x|$\frac{x-1}{x-4}>0$},则A∩B=( )
| A. | ∅ | B. | [2,4) | C. | [2,+∞) | D. | (4,+∞) |
6.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,1),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
13.在△ABC中,内角A、B、C所对的边分别为a、b、c,若$sin({\frac{3}{2}B+\frac{π}{4}})=\frac{{\sqrt{2}}}{2}$,且a+c=2,则△ABC周长的取值范围是( )
| A. | (2,3] | B. | [3,4) | C. | (4,5] | D. | [5,6) |
11.已知直线y=3-x与两坐标轴围成的区域为Ω1,不等式组$\left\{\begin{array}{l}y≤3-x\\ x≥0\\ y≥2x\end{array}\right.$所形成的区域为Ω2,现在区域Ω1中随机放置一点,则该点落在区域Ω2的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
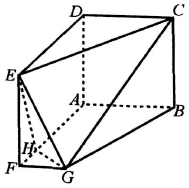 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.