题目内容
设集合A={x|x2-3x+2=0}，B={x|x2+（a+1）x+（a2-14）=0}，若A∩B=A，求实数a的值．
考点：集合的包含关系判断及应用
专题：集合
分析：本题的关键是根据集合A={x|x2-3x+2=0}，B={x|x2+（a+1）x+（a2-14）=0}，找到集合A、B的元素，再由A∩B=A等价于A⊆B可得a的值．
解答：
解：∵A={x|x2-3x+2=0}，
∴A={1，2}
又∵A∩B=A，
∴A⊆B
∵B={x|x2+（a+1）x+（a2-14）=0}，
∴x=1，2是方程x2+（a+1）x+（a2-14）=0的根
∴将x=1带入可得，实数a的值为：a=-4
∴A={1，2}
又∵A∩B=A，
∴A⊆B
∵B={x|x2+（a+1）x+（a2-14）=0}，
∴x=1，2是方程x2+（a+1）x+（a2-14）=0的根
∴将x=1带入可得，实数a的值为：a=-4
点评：本题主要考查集合包含基本运算，属于基础题．要正确判断两个集合间包含的关系，必须对集合的相关概念有深刻的理解，善于抓住代表元素，认清集合的特征．
练习册系列答案
小学课时特训系列答案
相关题目
函数若函数g（x）=asinxcosx（a＞0）的最大值为
，则函数f（x）=sinx+acosx的图象的一条对称轴方程为（ ）
| 1 |
| 2 |
| A、x=0 | ||
B、x=-
| ||
C、x=-
| ||
D、x=-
|
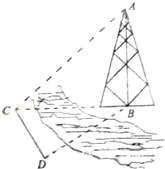如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=60°，∠BDC=75°，CD=50