题目内容
已知函数f(x)=
ax2+2lnx,曲线y=f(x)在x=1处的切线斜率为4.
(1)求a的值及切线方程;
(2)点P(x,y)为曲线y=f′(x)上一点,求y-x的最小值.
| 1 |
| 2 |
(1)求a的值及切线方程;
(2)点P(x,y)为曲线y=f′(x)上一点,求y-x的最小值.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:(1)求导函数,利用曲线y=f(x)在x=1处的切线斜率为4,建立方程,即可求a的值及切线方程;
(2)利用导函数,结合函数的定义域,利用基本不等式,即可求y-x的最小值.
(2)利用导函数,结合函数的定义域,利用基本不等式,即可求y-x的最小值.
解答:
解:(1)∵f(x)=
ax2+2lnx,∴f′(x)=ax+
…2分
∵曲线y=f(x)在x=1处的切线斜率为4,
∴f'(1)=a+2=4…3分
∴a=2…4分
∴f(1)=1…5分
∴切线方程为y-1=4(x-1),即4x-y-3=0…7分
(2)函数f(x)的定义域为(0,+∞)…8分
∵点P(x,y)为曲线y=f'(x)上一点,
∴y-x=x+
≥2
,当且仅当x=
时,等号成立.…12分
∴y-x的最小值为2
.…13分.
| 1 |
| 2 |
| 2 |
| x |
∵曲线y=f(x)在x=1处的切线斜率为4,
∴f'(1)=a+2=4…3分
∴a=2…4分
∴f(1)=1…5分
∴切线方程为y-1=4(x-1),即4x-y-3=0…7分
(2)函数f(x)的定义域为(0,+∞)…8分
∵点P(x,y)为曲线y=f'(x)上一点,
∴y-x=x+
| 2 |
| x |
| 2 |
| 2 |
∴y-x的最小值为2
| 2 |
点评:本题考查导数知识的运用,考查导数的几何意义,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x3+(b-|a|)x2+(a2-4b)x是奇函数,则f′(0)的最小值是( )
| A、-4 | B、0 | C、1 | D、4 |
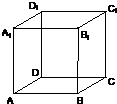 电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.
电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.