题目内容
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足r(x)=
假定该产品产销平衡,根据上述统计规律求:
(Ⅰ)要使工厂有盈利,产品数量x应控制在什么范围?
(Ⅱ)工厂生产多少台产品时盈利最大?
|
假定该产品产销平衡,根据上述统计规律求:
(Ⅰ)要使工厂有盈利,产品数量x应控制在什么范围?
(Ⅱ)工厂生产多少台产品时盈利最大?
考点:分段函数的应用
专题:应用题,函数的性质及应用
分析:(I)依题意得g(x)=x+3,设利润函数为f(x),根据f(x)=r(x)-g(x),可得f(x)=
,要使工厂有盈利,则有f(x)>0,解不等式可得结论;
(Ⅱ)分段求出函数的最值,比较可得结论.
|
(Ⅱ)分段求出函数的最值,比较可得结论.
解答:
解:依题意得g(x)=x+3,设利润函数为f(x),则f(x)=r(x)-g(x),
所以f(x)=
(2分)
(I)要使工厂有盈利,则有f(x)>0,
所以
或
,(4分)
所以3<x<10.5.(7分)
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内.(8分)
(II)当3<x≤7时,f(x)=-0.5(x-6)2+4.5
故当x=6时,f(x)有最大值4.5.(10分)
而当x>7时,f(x)<10.5-7=3.5.
所以当工厂生产600台产品时,盈利最大. (12分)
所以f(x)=
|
(I)要使工厂有盈利,则有f(x)>0,
所以
|
|
所以3<x<10.5.(7分)
所以要使工厂盈利,产品数量应控制在大于300台小于1050台的范围内.(8分)
(II)当3<x≤7时,f(x)=-0.5(x-6)2+4.5
故当x=6时,f(x)有最大值4.5.(10分)
而当x>7时,f(x)<10.5-7=3.5.
所以当工厂生产600台产品时,盈利最大. (12分)
点评:本题给出工厂生产的实际应用问题,求最大盈利时的产量x值,着重考查了基本初等函数的单调性、不等式的解法和用函数知识解决实际应用问题等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x3+(b-|a|)x2+(a2-4b)x是奇函数,则f′(0)的最小值是( )
| A、-4 | B、0 | C、1 | D、4 |
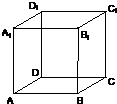 电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.
电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.