题目内容
3.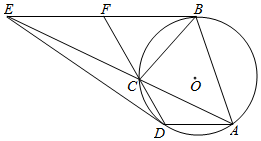 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.(1)证明:AB•CD=BC•AD;
(2)延长DC交BE于F,若EF=FB,证明:AD∥BE.
分析 (1)利用三角形的相似,结合切线长相等,即可证明:AB•CD=BC•AD;
(2)利用切割线定理,结合BF=EF,证明出△EFC∽△DFE,进而证明∠EFC=∠DAC,即可得出结论.
解答 证明:(1)∵过B、D两点的切线交于点E,
∴EB=ED,∠EBC=∠EAB,∠EDC=∠EAD
∵∠BEA=∠CEB,∠CED=∠DEA,
∴△EBC∽△EAB,△EDC∽△EAD,
∴$\frac{AB}{BC}=\frac{EA}{EB}$,$\frac{AD}{CD}=\frac{EA}{ED}$,
∴$\frac{AB}{BC}=\frac{AD}{CD}$,
∴AB•CD=BC•AD;
(2)∵BF2=FC•FD,BF=EF,
∴EF2=FC•FD,
∴$\frac{EF}{FC}=\frac{FD}{EF}$,
∵∠EFC=∠DFE,
∴△EFC∽△DFE,
∴∠FEC=∠FDE,
∵∠FDE=∠EAD,
∴∠EFC=∠DAC,
∴AD∥BE.
点评 本题考查圆的切线的性质,考查三角形相似的证明与性质的运用,证明三角形相似是关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
14.设i是虚数单位,若复数a+$\frac{1+i}{1-i}$(a∈R)是纯虚数,则a=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
18.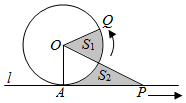 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
8.实数$\frac{a+i}{2-i}$(a为实数)的共轭复数为( )
| A. | 1 | B. | -5 | C. | -1 | D. | -i |
13.若an=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{n}^{2}+1}$(n∈N*),则a2等于( )
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1$+\frac{1}{2}$$+\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |