题目内容
18.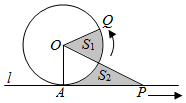 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
分析 由题意得,弧AQ的长度与AP相等,利用扇形的面积公式与三角形的面积公式表示出阴影部分的面积S1,S2,比较大小即可.
解答 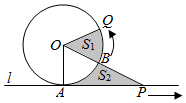 解:如图所示,
解:如图所示,
∵直线l与圆O相切,∴OA⊥AP,
∴S扇形AOQ=$\frac{1}{2}$•$\widehat{AQ}$•r=$\frac{1}{2}$•$\widehat{AQ}$•OA,
S△AOP=$\frac{1}{2}$•OA•AP,
∵$\widehat{AQ}$=AP,
∴S扇形AOQ=S△AOP,
即S扇形AOQ-S扇形AOB=S△AOP-S扇形AOB,
∴S1=S2.
故选:A.
点评 本题考查了切线的性质与扇形的面积公式的计算问题,解题时应熟练地掌握切线的性质与应用,是基础题目.

练习册系列答案
相关题目
6.等差数列{an}的前n项和为Sn,且满足2S3=a3+a7=18,则a1=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知复数z=$\frac{3+2i}{2-3i}$,则z的共轭复数$\overline z$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
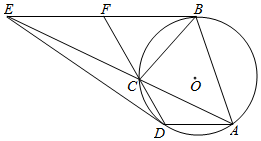 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.