题目内容
12.已知P为△ABC所在平面上的一点,且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+2y$\overrightarrow{AC}$,其中x,y∈R为实数,设点M(x,y),点N(1,1),当点P落在△ABC的内部,|MN|的取值范围是($\frac{2\sqrt{5}}{5}$,$\sqrt{2}$).分析 由P在△ABC内部可知$\left\{\begin{array}{l}{x>0}\\{2y>0}\\{0<x+2y<1}\end{array}\right.$,作出可行域,根据|MN|的几何意义求出|MN|的最大值和最小值.
解答 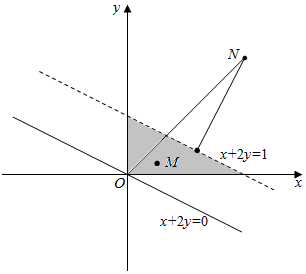 解:∵$\overrightarrow{AP}$=x$\overrightarrow{AB}$+2y$\overrightarrow{AC}$,点P落在△ABC的内部,
解:∵$\overrightarrow{AP}$=x$\overrightarrow{AB}$+2y$\overrightarrow{AC}$,点P落在△ABC的内部,
∴$\left\{\begin{array}{l}{x>0}\\{y>0}\\{0<x+2y<1}\end{array}\right.$,
作出约束条件表示的可行域如图:
由可行域可知|MN|的最小值为N到直线x+2y=1的距离d=$\frac{|1+2-1|}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$.
|MN|的最大值为|ON|=$\sqrt{2}$.
故答案为($\frac{2\sqrt{5}}{5}$,$\sqrt{2}$).
点评 本题考查了简单的线性规划,平面向量线性运算的几何意义,属于中档题.

练习册系列答案
相关题目
7.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?( )
| A. | 9日 | B. | 8日 | C. | 16日 | D. | 12日 |
4.函数f(x)=|sin2x|-sin2x的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
7.在正三棱锥S-ABC中,异面直线SA与BC所成角的大小为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.