题目内容
13.求抛物线$\left\{\begin{array}{l}{x=2t}\\{y=2{t}^{2}+1}\end{array}\right.$(t为参数)的准线的普通方程.分析 求出抛物线的普通方程,再求出准线方程.
解答 解:∵$\left\{\begin{array}{l}{x=2t}\\{y=2{t}^{2}+1}\end{array}\right.$(t为参数),∴$\left\{\begin{array}{l}{t=\frac{x}{2}}\\{{t}^{2}=\frac{y-1}{2}}\end{array}\right.$,
∴$\frac{y-1}{2}$=$\frac{{x}^{2}}{4}$,即x2=2(y-1).
∴抛物线的准线方程为y-1=-$\frac{1}{2}$,即y=$\frac{1}{2}$.
点评 本题考查了抛物线的参数方程与普通方程的转化,属于基础题.

练习册系列答案
相关题目
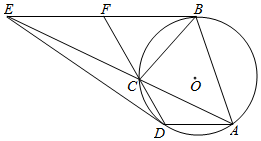 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.