题目内容
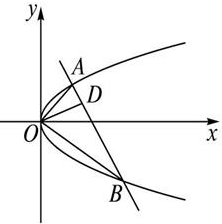
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50
,则抛物线的方程为( )
| 5 |

| A、y2=20x | ||
| B、y2=10x | ||
| C、y2=5x | ||
D、y2=
|
考点:直线与圆锥曲线的综合问题,抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及x1•x2+y1•y2=0消元,最后将面积之和表示出来,探求最值问题.
解答:
解:设直线AB的方程为:x=ty+m,点A(x1,y1),B(x2,y2),直线AB与x轴的交点为M(m,0),
x=ty+m代入y2=2px,可得y2-2pty-2pm=0,根据韦达定理有y1•y2=-2pm,
∵OA⊥OB,∴x1•x2+y1•y2=0,从而
(y1•y2)2+y1•y2=0,
∵点A,B位于x轴的两侧,
∴y1•y2=-4p2,故m=2p.
不妨令点A在x轴上方,则y1>0,
又F(
,0),
∴S△ABO+S△AFO=
×2p×(y1-y2)+
×
y1=
y1+
≥2
p2,
当且仅当
y1=
时,取“=”号,
∴2
p2=50
,∴p=5
故抛物线的方程为:y2=10x.
故选:B.
x=ty+m代入y2=2px,可得y2-2pty-2pm=0,根据韦达定理有y1•y2=-2pm,
∵OA⊥OB,∴x1•x2+y1•y2=0,从而
| 1 |
| 4p2 |
∵点A,B位于x轴的两侧,
∴y1•y2=-4p2,故m=2p.
不妨令点A在x轴上方,则y1>0,
又F(
| p |
| 2 |
∴S△ABO+S△AFO=
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| 5p |
| 4 |
| 4p3 |
| y1 |
| 5 |
当且仅当
| 5p |
| 4 |
| 4p3 |
| y1 |
∴2
| 5 |
| 5 |
故抛物线的方程为:y2=10x.
故选:B.
点评:求解本题时,应考虑以下几个要点:
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
在△ABC中,设角A,B,C的对边分别为a,b,c.已知B=45°,C=120°,b=2,则c=( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若一个正三棱柱的三视图如图所示,则这个正三棱柱的体积是( )


A、2
| ||
B、4
| ||
C、6
| ||
D、8
|
在区间[-2,3]中任取一个数m,则“方程
+
=1表示焦点在x轴上的椭圆”的概率是( )
| x2 |
| m+3 |
| y2 |
| m2+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
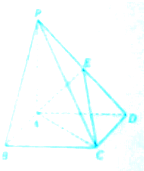 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,PA=AB,E为PO的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,PA=AB,E为PO的中点.