题目内容
已知圆C1:x2+y2=1与圆C2:(x-2)2+(y-4)2=5,过动点 P(a,b)分别作圆C1,圆C2的切线PM,PN( M、N分别为切点),若PM=PN,则(a-5)2+(b+1)2的最小值是 .
考点:直线与圆的位置关系
专题:直线与圆
分析:根据条件PM=PN,求出P的轨迹方程,(a-5)2+(b+1)2的几何意义为P到定点(5,-1)的距离的平方,即可得到结论.
解答:
解:∵过动点 P(a,b)分别作圆C1,圆C2的切线PM,PN( M、N分别为切点),若PM=PN,
∴|PC1|2-1=|PC2|2-5,
即a2+b2-1=(a-2)2+(b-4)2-5,
即a+2b-4=0,即动点P(a,b)在直线x+2y-4=0上,
(a-5)2+(b+1)2的几何意义为P到定点(5,-1)的距离的平方,
则点(5,-1)到直线x+2y-4=0的距离为
=
,
故(a-5)2+(b+1)2的最小值为
,
故答案为:
∴|PC1|2-1=|PC2|2-5,
即a2+b2-1=(a-2)2+(b-4)2-5,
即a+2b-4=0,即动点P(a,b)在直线x+2y-4=0上,
(a-5)2+(b+1)2的几何意义为P到定点(5,-1)的距离的平方,
则点(5,-1)到直线x+2y-4=0的距离为
| |5+2×(-1)-4| | ||
|
| ||
| 5 |
故(a-5)2+(b+1)2的最小值为
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题主要考查直线和圆的位置关系的应用,以及点到直线的距离公式的应用,利用距离的几何意义是解决本题的关键.

练习册系列答案
相关题目
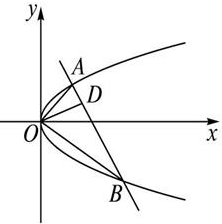
如图,一条直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50
,则抛物线的方程为( )
| 5 |

| A、y2=20x | ||
| B、y2=10x | ||
| C、y2=5x | ||
D、y2=
|
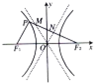 已知点P是双曲线C:
已知点P是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知函数f(x)=
和函数g(x)=2x-2-x.
(1)判断h(x)=
的奇偶性,并求其单调区间;
(2)若函数h(x)=f(x)+λg(x)是R上的增函数,求实数λ的取值范围.
| 4x+1 |
| 2x |
(1)判断h(x)=
| f(x) |
| g(x) |
(2)若函数h(x)=f(x)+λg(x)是R上的增函数,求实数λ的取值范围.
设i为虚数单位,则复数
=( )
| 3-4i |
| i |
| A、-4-3i | B、-4+3i |
| C、4+3i | D、4-3i |
若双曲线
-y2=1(a>0)的离心率为2,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| A、y=±x | ||||
| B、y=±3x | ||||
C、y=±
| ||||
D、y=±
|