题目内容
已知圆E:(x-1)2+(y-2)2=25直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明不论m取什么实数,直线与圆恒交于两点;
(2)设P(x,y)是圆E上任意一点,求x+y的取值范围.
(3)已知AC、BD为圆C的两条相互垂直的弦,垂足为M(3,1),求四边形ABCD的面积的最大值.
(1)证明不论m取什么实数,直线与圆恒交于两点;
(2)设P(x,y)是圆E上任意一点,求x+y的取值范围.
(3)已知AC、BD为圆C的两条相互垂直的弦,垂足为M(3,1),求四边形ABCD的面积的最大值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)求出直线l:(2m+1)x+(m+1)y-7m-4=0恒过定点,确定点在圆E内,即可得出结论;
(2)利用参数法,表示x+y,利用辅助角公式化简,即可求x+y的取值范围.
(3)利用四边形ABCD的面积S=
|AC||BD|,结合基本不等式,即可求四边形ABCD的面积的最大值.
(2)利用参数法,表示x+y,利用辅助角公式化简,即可求x+y的取值范围.
(3)利用四边形ABCD的面积S=
| 1 |
| 2 |
解答:
(1)证明:直线l:(2m+1)x+(m+1)y-7m-4=0可化为(x+y-4)+m(2x+y-7)=0,
∵m∈R,∴x+y-4=0,且2x+y-7=0,得x=3,y=1,
即l恒过定点M(3,1).
∵圆心E(1,2),|ME|=
<5,
∴点M在圆E内,从而直线l恒与圆E相交于两点.
(2)解:设x=1+5cosα,y=2+5sinα,则x+y=3+5(cosα+sinα)=3+5
sin(α+θ)∈[3-5
,3+5
];
(3)解:设圆心E到AC,BD的距离分别为d1,d2,则d12+d22=EM=5,
∴四边形ABCD的面积S=
|AC||BD|=2
≤50-(d12+d22)=45.
∵m∈R,∴x+y-4=0,且2x+y-7=0,得x=3,y=1,
即l恒过定点M(3,1).
∵圆心E(1,2),|ME|=
| 5 |
∴点M在圆E内,从而直线l恒与圆E相交于两点.
(2)解:设x=1+5cosα,y=2+5sinα,则x+y=3+5(cosα+sinα)=3+5
| 2 |
| 2 |
| 2 |
(3)解:设圆心E到AC,BD的距离分别为d1,d2,则d12+d22=EM=5,
∴四边形ABCD的面积S=
| 1 |
| 2 |
| (25-d12)(25-d22) |
点评:本题考查直线与圆的位置关系,考查参数法的运用,考查四边形面积的计算,属于中档题.

练习册系列答案
相关题目
已知α,β是方程x2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a∈R,b∈R,求
的最大值与最小值之和为( )
| b-3 |
| a-3 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
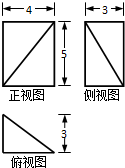

| A、10cm3 |
| B、20cm3 |
| C、30cm3 |
| D、40cm3 |