题目内容
 红旗化肥厂生产A、B两种化肥.某化肥销售店从该厂买进一批化肥,每种化肥至少购买5吨,每吨出厂价分别为2万元、1万元.且销售店老板购买
红旗化肥厂生产A、B两种化肥.某化肥销售店从该厂买进一批化肥,每种化肥至少购买5吨,每吨出厂价分别为2万元、1万元.且销售店老板购买化肥资金不超过30万元.
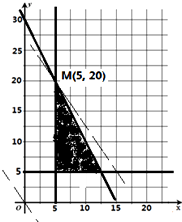
(Ⅰ)若化肥销售店购买A、B两种化肥的数量分别是x(吨)、y(吨),写出x、y满足的不等式组;并在给定的坐标系中画出不等式组表示的平面区域(用阴影表示);
(Ⅱ)假设该销售店购买的A、B这两种化肥能全部卖出,且每吨化肥的利润分别为 0.3万元、0.2万元,问销售店购买A、B两种化肥各多少吨时,才能获得最大利润,最大利润是多少万元?
考点:简单线性规划的应用
专题:计算题,应用题,作图题,不等式的解法及应用
分析:(Ⅰ)由题意可写出不等式组
,从而作出平面区域;
(Ⅱ) 设销售店出售这两种化肥的总利润为z万元,则目标函数为z=0.3x+0.2y,利用线性规划求最值.
|
(Ⅱ) 设销售店出售这两种化肥的总利润为z万元,则目标函数为z=0.3x+0.2y,利用线性规划求最值.
解答:
 解:(Ⅰ)依题意,x、y满足的不等式组如下:
解:(Ⅰ)依题意,x、y满足的不等式组如下:
,
画出的平面区域
(Ⅱ) 设销售店出售这两种化肥的总利润为z万元,
则目标函数为z=0.3x+0.2y,
即y=-
x+5z,5z表示过可行域内的点,斜率为-
的一组平行线在y轴上的截距.
联立
,
解得
即M(5,20),
当直线过点M(5,20)时,在y轴上的截距最大,
即Z的最大值为0.3×5+0.2×20=5.5(万元),
故销售店购买A、B两种化肥分别为5吨、20吨时,才能使利润最大,最大利润为5.5万元.
 解:(Ⅰ)依题意,x、y满足的不等式组如下:
解:(Ⅰ)依题意,x、y满足的不等式组如下:
|
画出的平面区域
(Ⅱ) 设销售店出售这两种化肥的总利润为z万元,
则目标函数为z=0.3x+0.2y,
即y=-
| 3 |
| 2 |
| 3 |
| 2 |
联立
|
解得
|
当直线过点M(5,20)时,在y轴上的截距最大,
即Z的最大值为0.3×5+0.2×20=5.5(万元),
故销售店购买A、B两种化肥分别为5吨、20吨时,才能使利润最大,最大利润为5.5万元.
点评:本题考查了实际问题转化为数学问题的能力及线性规划的应用,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若实数x,y满足
,则z=3x+2y的值域是( )
|
| A、[0,6] |
| B、[1,9] |
| C、[2,8] |
| D、[3,7] |
若不等式x2+kx+1<0的解集为空集,则k的取值范围是( )
| A、[-2,2] |
| B、(-∞,-2]∪[2,+∞) |
| C、(-2,2) |
| D、(-∞,-2)∪(2,+∞) |
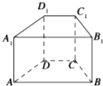 如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件
如图所示,在直四棱柱ABCD-A1B1C1D1中,当底面四边形A1B1C1D1满足条件