Question

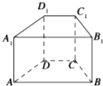如图所示，在直四棱柱ABCD-A₁B₁C₁D₁中，当底面四边形A₁B₁C₁D₁满足条件

 

时，有A₁C⊥B₁D₁（注：填上你认为正确的一种情况即可，不必考虑所有可能的情况）．

Answer 1

考点：直线与平面垂直的性质

专题：开放型,空间位置关系与距离

分析：由假设A₁C⊥B₁D₁，结合直四棱柱的性质及线面垂直的判定和性质定理，我们易得到A₁C₁⊥B₁D₁，即AC⊥BD，又由菱形的几何特征可判断出四边形ABCD为菱形，又由本题为开放型题目上，故答案可以不唯一．

解答： 解：若A₁C⊥B₁D₁，由四棱柱ABCD-A₁B₁C₁D₁为直四棱柱，
AA₁⊥B₁D₁，易得B₁D₁⊥平面AA₁BB₁，
则A₁C₁⊥B₁D₁，即AC⊥BD，
则四边形ABCD为菱形，
故答案为：AC⊥BD或四边形ABCD为菱形．

点评：本题主要考查了空间中直线与直线之间的位置关系，属于知识的考查，属于中档题．