题目内容
19.已知△ABC中,D在边BC上,且BD=4,DC=2,∠B=60°,∠ADC=150°.(1)求AC的长;
(2)求△ABC的面积.
分析 (1)根据余弦定理即可求出AC的长,
(2)根据三角形的面积公式计算即可
解答 解:(1)在△ABD中,∠BAD=150°-60o=90o,∴AD=4sin60°=2$\sqrt{3}$.
在△ACD中,由余弦定理得,AC2=(2$\sqrt{3}$)2+22-2×2$\sqrt{3}$×2×cos150°=28,
∴AC=2$\sqrt{7}$
(2)△ABD中,AB=4cos60°=2.S△ABC=$\frac{1}{2}$×2×6×sin60°=$3\sqrt{3}$.
点评 本题考查三角形的余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
9.复数z=(1-i)(4-i)的共轭复数的虚部为( )
| A. | -5i | B. | 5i | C. | -5 | D. | 5 |
10.下列命题中的真命题是( )
| A. | ?x0∈R,使得sinx+cosx=$\frac{3}{2}$ | B. | ?x0∈R,使得$x_0^2-{x_0}+1=0$ | ||
| C. | ?x∈(0,+∞),ex>x+1 | D. | ?x∈(0,π),sinx>cosx |
4.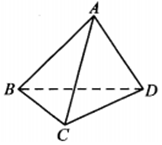 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
 在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
在四面体ABCD中,二面角A-BC-D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )| A. | θ的最大值为60° | B. | θ的最小值为60° | C. | θ的最大值为30° | D. | θ的最小值为30° |
11.抛物线y2=4x上有两点A、B到焦点的距离之和为8,则A、B到y轴的距离之和为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
8.设A(1,1)、B(7,4),点C满足$\overrightarrow{AC}$=2$\overrightarrow{CB}$,则点C的坐标是( )
| A. | (3,2) | B. | (3,5) | C. | (5,3) | D. | (8,5) |
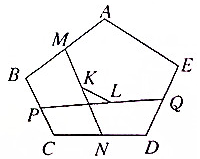 如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.
如图所示,五边形ABC 中,点M、N、P、Q分别是AB、CD、BC、DE的中点,K和L分别是MN和PQ的中点.求证:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.